2022. 1. 26. 17:10ㆍAlgorithm
학습목표
1. 최소비용 신장 트리(Minimum Spanning Tree, MST)가 무엇인지 학습
2. Generic MST 알고리즘에 대해서 학습
3. 안전한 에지가 무엇인지 학습
1. 최소비용 신장 트리(Minimum Spanning Tree, MST)가 무엇인가?
최소비용 신장 트리는 무방향 가중치 그래프에서 n개의 노드들을 최소의 비용만으로 서로 연결한 트리입니다. 예를 들어 아래의 그림은 무방향 가중치 그래프입니다.

위의 그림에서 가중치의 합이 최소가 되고 모든 노드들이 연결되는 해를 찾아야 합니다. 아래의 그림은 이러한 해 중에 하나입니다.
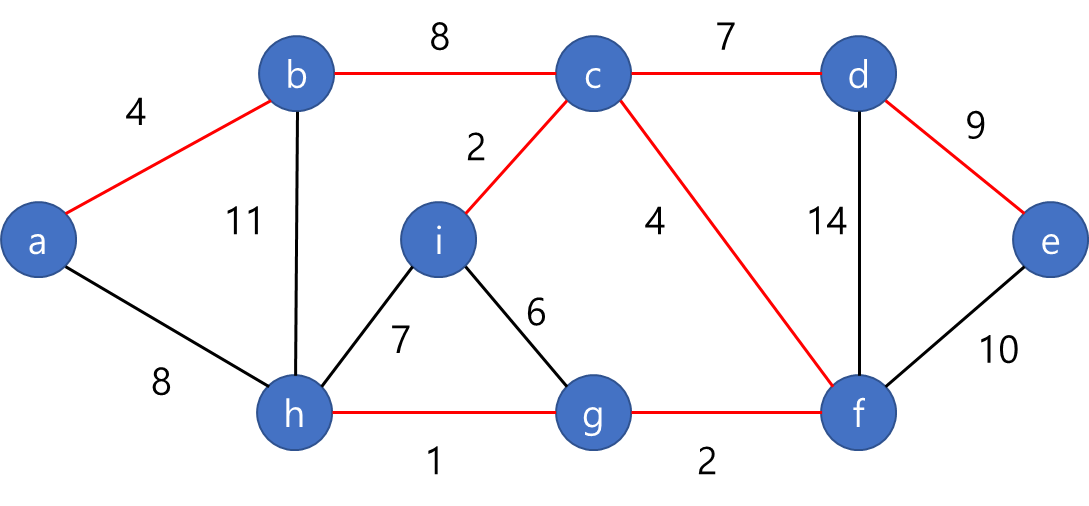
위의 그림은 최소 비용 신장 트리가 되는 해중에 하나인데 해는 유일하지는 않습니다. 예를 들어 (b,c) 에지 대신 (a,h) 에지를 연결 할 수도 있습니다.
트리의 정의
최소 비용 신장 트리 또한 하나의 트리인데 이를 그래프의 관점에서 정의하면 싸이클이 없는 연결된(connected) 무방향 그래프라고 정의할 수 있습니다. 이러한 트리는 노드가 n개인 트리는 항상 n-1개의 에지를 가지는 특징이 있습니다.
정리하면 최소 비용 신장 트리는 싸이클이 없는 연결된 무방향 그래프이고 n개의 노드들을 최소의 비용으로 에지들을 연결한 트리입니다.
2. Generic MST 알고리즘
- 어떤 MST의 부분집합 A(고른 에지(Edge)들)에 대해서 A U { (u,v) }도 역시 어떤 MST의 부분집합이 될 경우 에지 (u,v)는 A에 대해서 안전하다(safe)고 한다.
- Generic MST 알고리즘 수행과정
- 처음에는 부분집합 A는 공집합 ( A = ø)
- 집합 A에 대해서 안전한 에지를 하나 찾은 후 이것을 A에 더함
- 에지의 개수가 n-1개가 될 때까지 2번을 반복함
GENERIC-MST(G,w)
{
A <- ø
while A가 최소비용신장 트리가 아닐때동안만 반복
집합 A에 대해서 에지 (u,v)가 안전한지 검사
A <- A U {(u,v)} 집합 A에 에지 (u,v) 추가
return A
}
3. 안전한 에지(Edge) 탐색
안전한 에지를 정의하기 전에 Cut, Cross, Respect이라는 용어를 정의해야 합니다.
Cut
그래프의 노드들을 두 개의 집합 S와 V-S로 분할한 것을 Cut이라고 부릅니다. 그래프에서 노드들의 집합 V가 존재할때 V-S는 V집합에서 S집합을 차집합한 것입니다. 예를 들어 (S,V-S)는 다음과 같습니다.
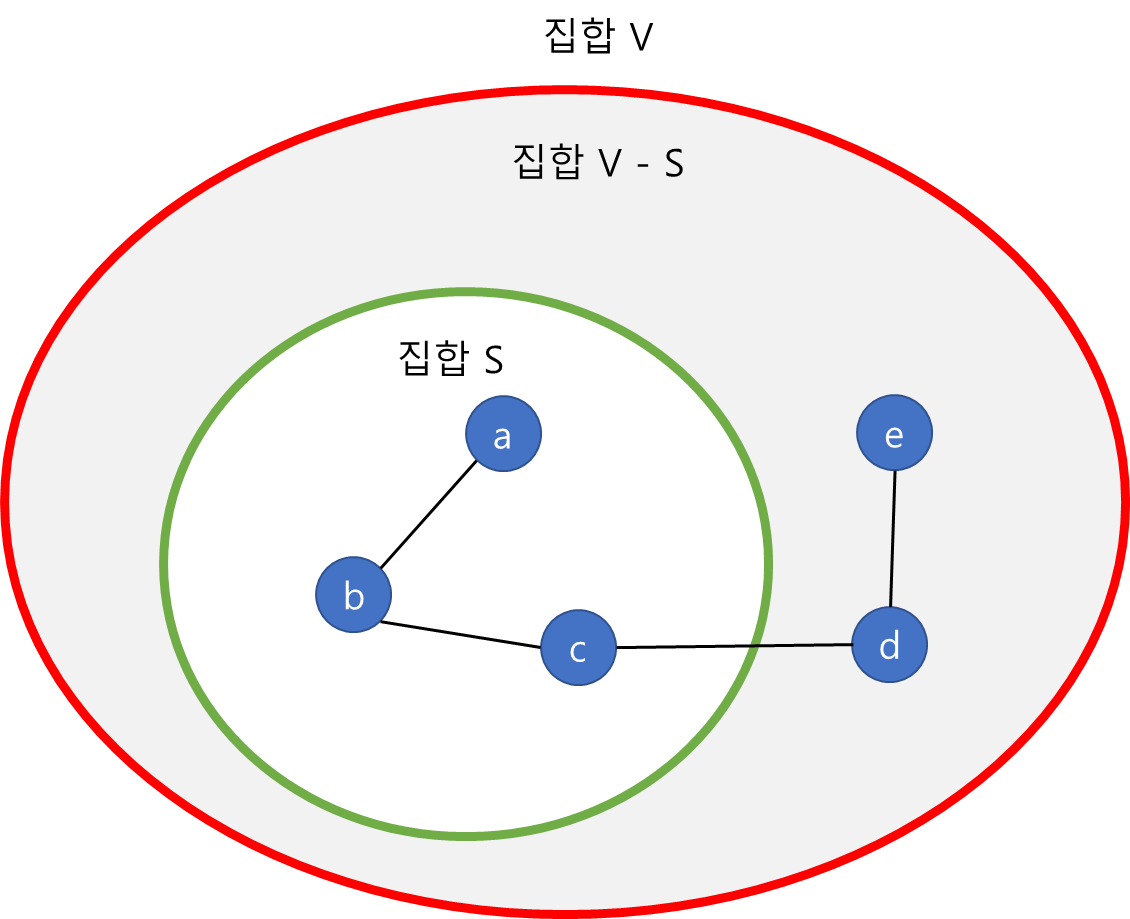
- V = {a,b,c,d,e}
- S = {a,b,c}
- V-S = {d,e}
Cross
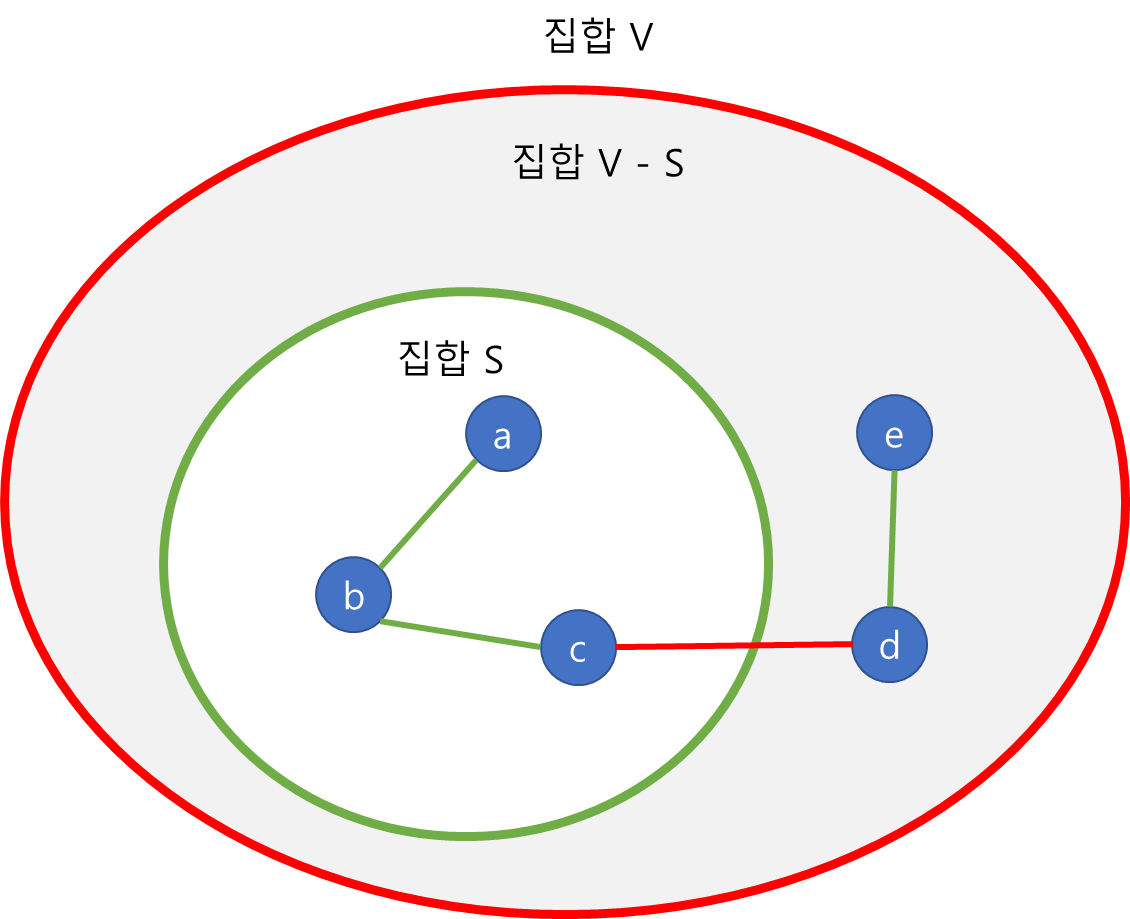
에지 (u,v)에 대해서 u∈S이고 v∈V-S일때 에지 (u,v)는 Cut (S,V-S)을 Cross한다고 말합니다. 즉, 정리하면 그래프에서 노드들의 집합인 V를 Cut하게 되면 집합 S, 집합 V-S가 되는데 이러한 상태에서 집합 S에 속하는 노드 u와 집합 V-S에 속하는 노드 v가 에지로 연결되어 있다면 이 에지 (u,v)는 Cross 한다고 말하는 것입니다. 예를 들어 아래의 그림에서 노드 c, 노드 d는 에지로 연결되어 있는데 이러한 에지 (c,d)가 Cross한다고 말하는 것입니다.

Respect
에지들의 부분집합 A에 속한 어떤 에지이고 Cut (S, V-S)를 Cross 하지 않을 때 Cut (S,V-S)는 A를 Respect 한다고 말할 수 있습니다. 예를 들어 아래 그림을 보시면 집합 S에서 에지 (a,b), (b,c)는 집합 S의 원소들끼리만 에지를 맺는 것을 볼 수 있습니다. 이러한 에지 (a,b), (b,c)는 부분집합 A를 Respect한다고 볼 수 있습니다. 그리고 집합 V-S에서 에지 (e,d)또한 집합 V-S의 원소들과 에지를 맺었으므로 에지 (e,d)는 부분집합 A를 Respect합니다. 그러나 에지 (c,d)에서 c는 집합 S의 원소이고 d는 집합 V-S의 원소입니다. 이러한 에지는 서로 집합이 다르기 때문에 Cross한다고 볼 수 있습니다. 에지 (c,d)는 Cross하였기 때문에 부분 집합 A를 Respect하지 않습니다.
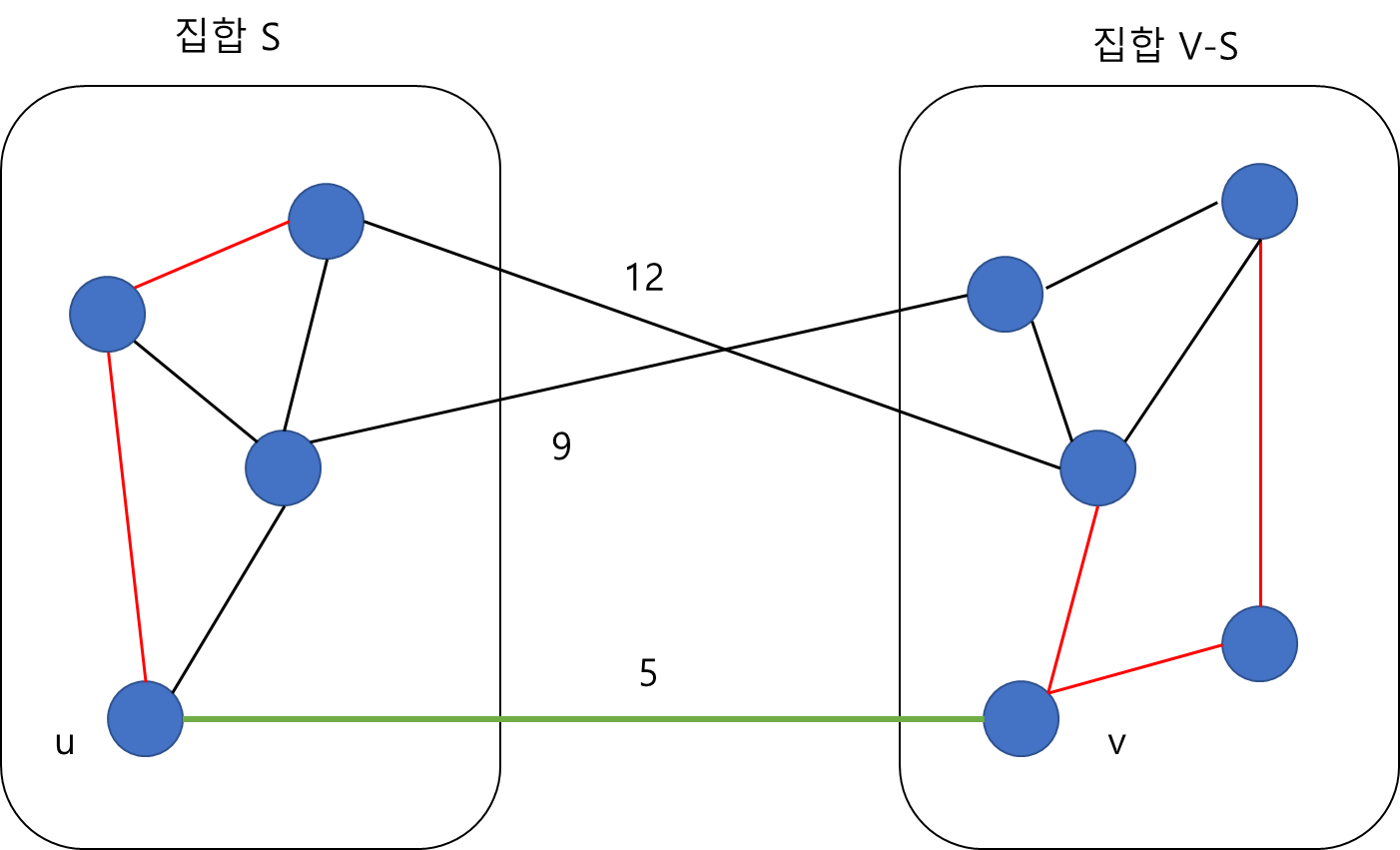
안전한 에지란 무엇인가
위의 Cut, Cross, Respect이라는 용어를 사용하여 안전한 에지를 정의하면 부분집합 A가 어떤 최소비용 신장 트리의 부분집합이고, Cut (S, V-S)는 부분집합 A를 존중하는 Cut이라고 가정합니다. 이 Cut을 Cross하는 에지들 중 가장 가중치가 작은 에지 (u,v)가 부분집합 A에 대해서 안전한 에지입니다. 예를 들어 아래의 그림에서 안전한 에지는 Cross하는 에지들 중 가장 가중치가 적은 에지는 에지 (u,v)입니다. 아래 그림에서 빨간색 에지들은 부분집합 A를 Respect하는 에지들입니다. 그리고 초록색 에지는 Cross하는 에지입니다.
정리하면 Generic MST 알고리즘은 부분집합 A에 안전한 에지들을 탐색한 다음 더하는 것을 반복(부분집합 A의 원소개수가 n-1개가 될때까지)하는 알고리즘입니다.
그리고 이러한 안전한 에지란 두 집합 S와 V-S가 존재할때 Cross하는 에지들 중 가장 가중치가 적은 에지가 부분집합 A한테 안전한 에지입니다.
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][Graph] 싸이클(Cycle) #1 방향 그래프에서 싸이클이 있는지 탐색하기 (0) | 2022.02.07 |
|---|---|
| [알고리즘][Graph] 최소 비용 신장 트리 #2 크루스칼(Kruskal) 알고리즘 개념 및 수행과정 (0) | 2022.01.27 |
| [알고리즘][Graph] DAG(Directed Acyclic Graph)와 위상 정렬(Topological ordering) (0) | 2022.01.25 |
| [알고리즘][Graph] 그래프의 순회 : DFS(Depth-First Search) 개념 및 수행과정 (0) | 2022.01.20 |
| [알고리즘][Graph] 그래프(Graph)의 순회 : BFS(Breadth-First Search) 개념 및 수행과정 (0) | 2022.01.19 |