2022. 2. 7. 15:31ㆍAlgorithm
학습목표
1. 방향 그래프에서 싸이클이 있는지 탐색하는것을 학습
1. 싸이클(Cycle)이란 무엇인가?
그래프의 특정 노드에서 출발하여 방향(Edge)를 따라 다시 출발한 노드로 올 수 있는 상황을 싸이클이 있다고 합니다.
아래의 그림은 싸이클이 있는 그래프와 없는 그래프를 표현한 것입니다. 왼쪽이 싸이클이 존재하는 그래프이고 오른쪽이 싸이클이 존재하지 않는 그래프입니다.

2. 싸이클을 탐색하기 위한 접근 방법 및 수행과정
한 그래프에는 0개 이상의 연결된(connected) 트리들이 존재할 것입니다. 이러한 트리들에 대해서 DFS(Depth First Search, 깊이우선탐색) 순회 방법을 사용하여 그래프의 싸이클을 탐색할 수 있습니다. DFS의 수행과정은 아래 글과 같습니다.
https://yonghwankim-dev.tistory.com/219?category=976238
[알고리즘][Graph] 그래프의 순회 : DFS(Depth-First Search) 개념 및 수행과정
학습목표 1. DFS은 무엇인지 학습 2. DFS의 수행과정을 학습 3. DFS의 시간복잡도에 대해서 학습 1. DFS(Depth-First Search, 깊이우선탐색)이란 무엇인가? DFS는 그래프의 순회 방법 중 하나로써 특정 노드에
yonghwankim-dev.tistory.com
방향 그래프에 싸이클이 존재하는지 탐색하기 위한 알고리즘 수행과정은 다음과 같습니다.
- 특정 노드에서 dfs 순회를 시작합니다.
- 시작 노드를 방문처리하고 재귀 스택 배열에도 true로 체크합니다.
- 시작한 노드의 인접 노드에 대해서 싸이클 검사를 수행합니다.
- 방문한 인접 노드가 이미 재귀 스택 배열에 체크(true)되어 있다면 싸이클 존재하므로 true를 반환합니다. 아니라면 방문한 인접 노드가 방문하였는지 검사하고 방문하지 않았다면 방문처리(true)합니다. 물론 재귀 스택 배열에도 true로 체크합니다.
- 모든 노드가 방문할때까지 1~4번 과정을 반복합니다.
위 알고리즘에서 핵심적인 것은 싸이클이 존재하는지 검사하는 재귀 스택 배열(recStack)입니다. DFS 순회중에서 특정 노드(A)가 인접 노드(B,C,D,E, ...)에 대해서 싸이클 검사를 마치기도 전에 다른 노드(B,C,D,E, ...)에서 특정 노드(A)를 인접 노드로 삼아 검사를 수행한다면 이는 특정 노드와 인접 노드간에 싸이클이 있다는 것을 의미합니다.
위 싸이클 검사 알고리즘의 수행과정을 그림으로 표현하면 다음과 같습니다. 아래의 그림은 방향그래프에서 싸이클이 존재하는 그래프입니다.


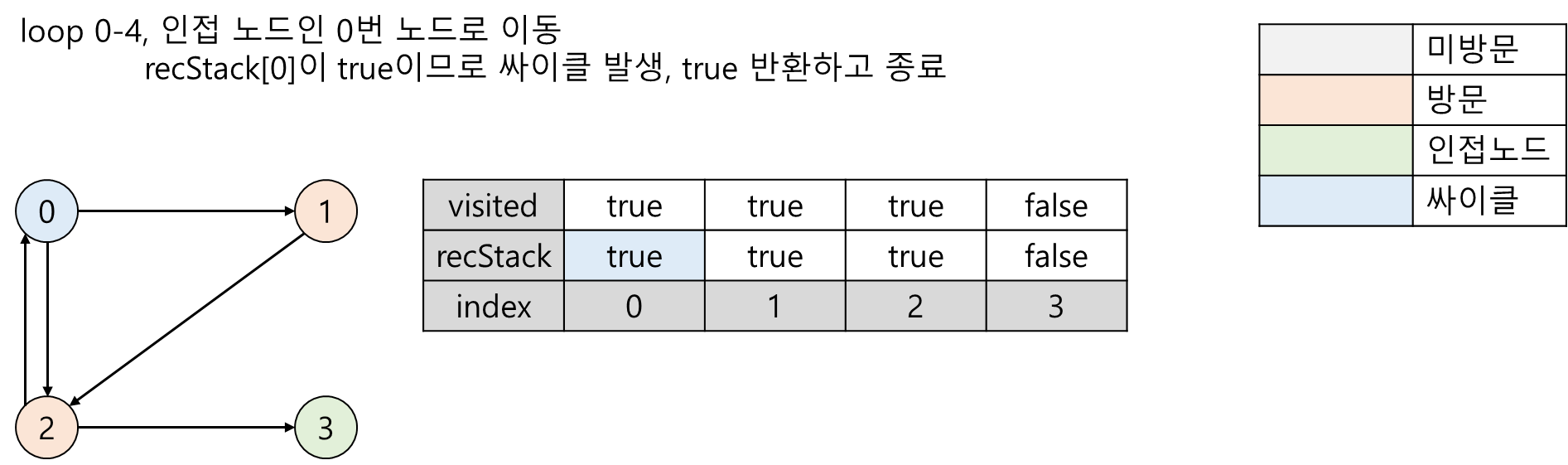
loop 0-4에서 2번 노드는 인접 노드인 0번 노드로 이동하였습니다. 0번 노드 입장에서는 아직 인접 노드의 싸이클 검사가 끝나기도 전에 다른 노드가 자신을 방문한 것이므로 visited[0]=true이고 인접노드의 싸이클 검사가 끝나지 않았으므로 recStack[0]=true입니다. 따라서 recStack[0]=true이므로 싸이클이 존재하여 true를 반환합니다. 이때 바로 종료되는 것이 아닌 순환호출 특성상 0번 노드로 회귀하면서 false를 반환합니다.
다음 예제는 방향 그래프에서 싸이클이 존재하지 않을때 수행과정입니다.





위 예제에서 방향 그래프는 싸이클이 존재하지 않으므로 0번 노드에서 DFS 순회를 시작하여 3번 노드로 이동합니다. 3번 노드에서 더 이상 인접 노드가 존재하지 않기 때문에 recStack 배열에서 자신의 노드에 해당하는 자리의 값을 false로 저장하면서 자신이 호출되었던 노드로 회귀합니다. 그리고 마지막으로 0번 노드에서도 false로 저장하면서 싸이클이 존재하지 않았으므로 false를 반환하면서 종료합니다.
3. Java 언어 기반 싸이클 탐색 구현
public class DirectedGraph<E> implements Graph<E>{
private int V; // 노드 개수
private ArrayList<ArrayList<Node<E>>> adj; // 인접리스트
private Map<Integer,E> map;
public DirectedGraph(int v) {
V = v;
adj = new ArrayList<ArrayList<Node<E>>>(v);
for(int i=0;i<v;i++)
{
adj.add(new ArrayList<Node<E>>());
}
map = new HashMap<Integer, E>();
}
public boolean isCyclic()
{
boolean[] visited = new boolean[V];
boolean[] recStack = new boolean[V];
for(int i=0;i<V;i++)
{
if(isCyclicUtil(i, visited, recStack))
{
return true;
}
}
return false;
}
private boolean isCyclicUtil(int i, boolean[] visited, boolean[] recStack)
{
if(recStack[i])
{
return true;
}
if(visited[i])
{
return false;
}
visited[i] = true;
recStack[i] = true;
Iterator<Node<E>> itor = adj.get(i).iterator();
while(itor.hasNext())
{
int adjNode = itor.next().getNum();
if(isCyclicUtil(adjNode, visited, recStack))
{
return true;
}
}
recStack[i] = false;
return false;
}
@Override
public void addEdge(Node u, Node v) {
if(!map.containsKey(u.getNum()))
{
map.put(u.getNum(), (E) u.getValue());
}
if(!map.containsKey(v.getNum()))
{
map.put(v.getNum(), (E) v.getValue());
}
adj.get(u.getNum()).add(v);
}
public static void main(String[] args)
{
int V = 4;
DirectedGraph<Integer> directedGraph = new DirectedGraph<Integer>(V);
Node<Integer> node0 = new Node<Integer>(0, 0);
Node<Integer> node1 = new Node<Integer>(1, 1);
Node<Integer> node2 = new Node<Integer>(2, 2);
Node<Integer> node3 = new Node<Integer>(3, 3);
directedGraph.addEdge(node0, node1);
directedGraph.addEdge(node0, node2);
directedGraph.addEdge(node1, node2);
directedGraph.addEdge(node2, node0);
directedGraph.addEdge(node2, node3);
if(directedGraph.isCyclic())
{
System.out.println("이 그래프는 싸이클이 존재합니다.");
}
else
{
System.out.println("이 그래프는 싸이클이 존재하지 않습니다.");
}
}
}이 그래프는 싸이클이 존재합니다.
4. 방향 그래프 싸이클 탐색 시간복잡도
- 시간복잡도 : O(V+E), V는 정점의 개수, E는 간선의 개수를 의미합니다. DFS 순회를 이용하기 때문에 V개의 정점들을 방문하고 인접노드 탐색으로 인하여 최악의 경우 E개의 개수만큼 간선을 확인합니다.
- 공간복잡도 : O(V), V는 정점의 개수를 의미합니다. 방문 배열(visited)에 정점의 개수만큼의 공간이 필요합니다.
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph05_iscycle
geeks for geeks : https://www.geeksforgeeks.org/detect-cycle-in-a-graph/
'Algorithm' 카테고리의 다른 글
| [알고리즘][Graph] Disjoint Set #1 무방향 그래프에서 싸이클 탐색 (0) | 2022.02.08 |
|---|---|
| [알고리즘][Graph] 싸이클(Cycle) #2 무방향 그래프에서 싸이클이 있는지 탐색 (0) | 2022.02.07 |
| [알고리즘][Graph] 최소 비용 신장 트리 #2 크루스칼(Kruskal) 알고리즘 개념 및 수행과정 (0) | 2022.01.27 |
| [알고리즘][Graph] 최소 비용 신장 트리 #1 최소 비용 신장 트리의 개념 (0) | 2022.01.26 |
| [알고리즘][Graph] DAG(Directed Acyclic Graph)와 위상 정렬(Topological ordering) (0) | 2022.01.25 |