2022. 1. 25. 12:31ㆍAlgorithm
학습목표
1. DAG(Directed Acyclic Graph)에 대해서 학습
2. 위상 정렬에 대해서 학습
3. 위상 정렬 알고리즘의 수행과정을 학습
4. 위상 정렬 알고리즘 구현
1. DAG(Directed Acyclic Graph)란 무엇인가?
DAG는 방향 사이클(directed cycle)이 없는 방향 그래프를 의미합니다. 방향 사이클이란 어느 특정 노드에서 시작하여 순회하고 다시 시작한 노드로 돌아올 수 있다면 그 그래프는 방향 사이클이 존재하는 그래프입니다. 아래의 그림은 방향 사이클이 존재하는 그래프입니다.

반대로 DAG는 방향 사이클이 없기 없는 방향 그래프이기 때문에 어느 특정 노드에서 시작하여도 다시 시작한 노드로 돌아 올 수 없습니다. 아래의 그림은 방향 사이클이 없는 방향 그래프입니다.

위의 그림을 보면 a노드에서 시작하여 순회한다고 가정하면 f까지 순회하는 가능은 하지만 방향 그래프이기 때문에 다시 되돌아 갈 수는 없는 것을 볼 수 있습니다.
DAG를 사용하는 이유
DAG를 사용하는 이유는 작업들의 우선순위를 표현하기 좋기 때문입니다. 예를 들어 여러개의 작업들이 존재하는데 어떤 작업은 그에 앞서서 선행되어야 하는 선행 작업이 존재 할 수 있습니다. 위의 DAG 예의 그림에서 노드 e가 하나의 작업이라면 노드 e를 완수하기 위해서는 노드 b,d가 먼저 수행되어야 합니다.
노드 e가 만약 완료되었다면 다음 작업으로 노드 c 또는 노드 f를 다음 작업으로 선택할 수 있습니다.
정리하면 DAG는 방향 사이클이 없는 그래프이고 DAG를 사용하는 이유는 작업들의 우선순위를 표현하기 좋기 때문입니다.
2. 위상 정렬(Topological ordering)이란 무엇인가?
위상 정렬이란 DAG에서 노드들을 순서화(v₁, v₂, ..., v_n) 시키는 것입니다. 단, 모든 에지 (v_i, v_j)에 대해서 i<j가 되도록 해야합니다. 이는 j가 i와 같거나 작을때 방향 사이클이 발생되기 때문입니다.

위의 그림에서 오른쪽 하단은 위 그래프에 대한 여러 가지 위상 정렬에서 예시 2가지를 표현한 것입니다. 작업들의 우선순위는 a->g->d->b->e->c->f의 순서로 갈수도 있고 a->b->g->d->e->f->c의 순서로 작업을 완수 할 수 있습니다. 여기서 작업을 완수한다는 의미는 노드를 방문하여 순회한다는 의미로도 해석될 수 있습니다.
대표적인 특징은 노드들의 에지 방향이 전부 오른쪽으로 선형적으로 간다는 것입니다. 여기서 만약 왼쪽 방향이 생긴다면 그것은 방향 사이클이 생긴다는 것을 의미합니다.
3. 위상 정렬 알고리즘의 수행과정
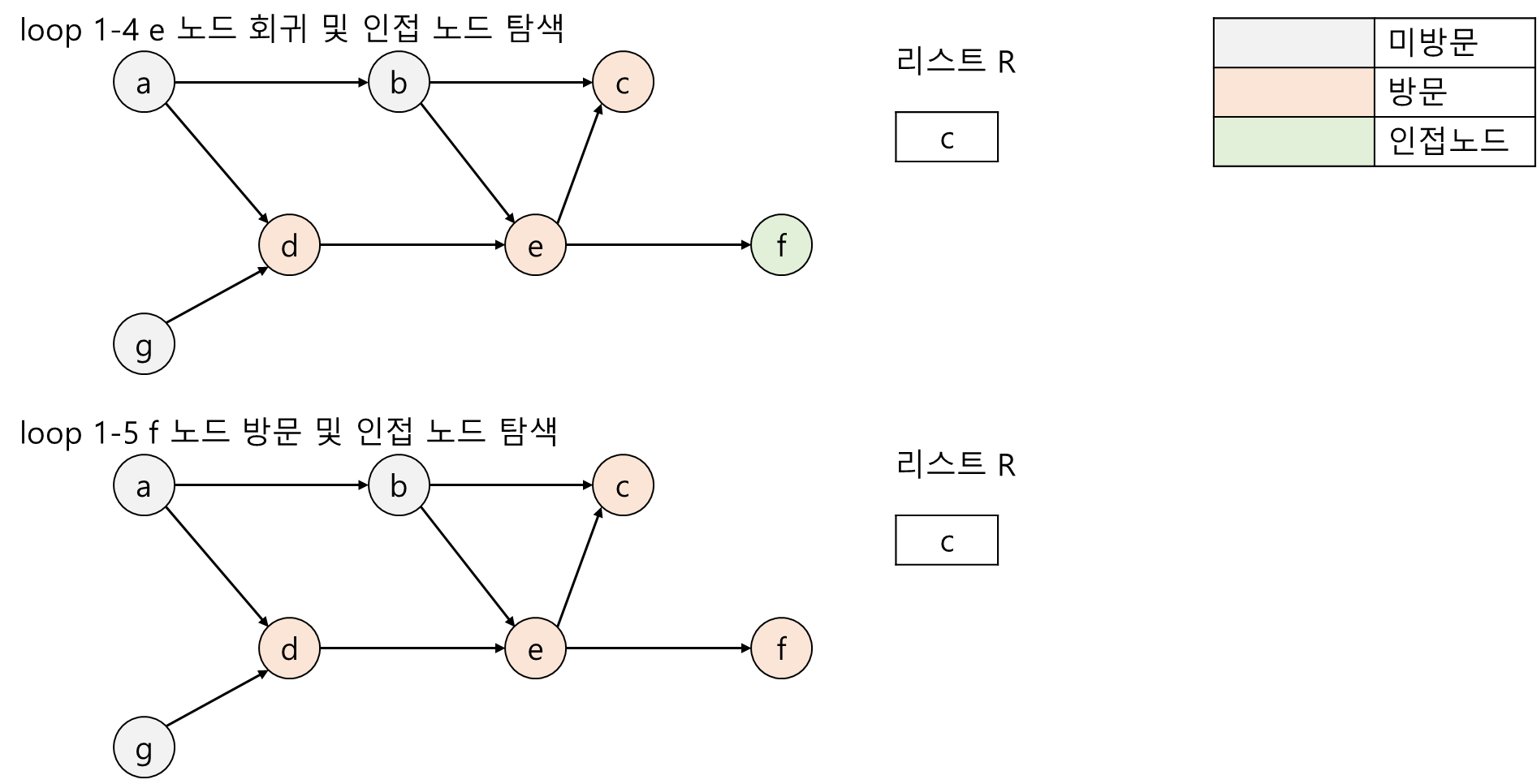
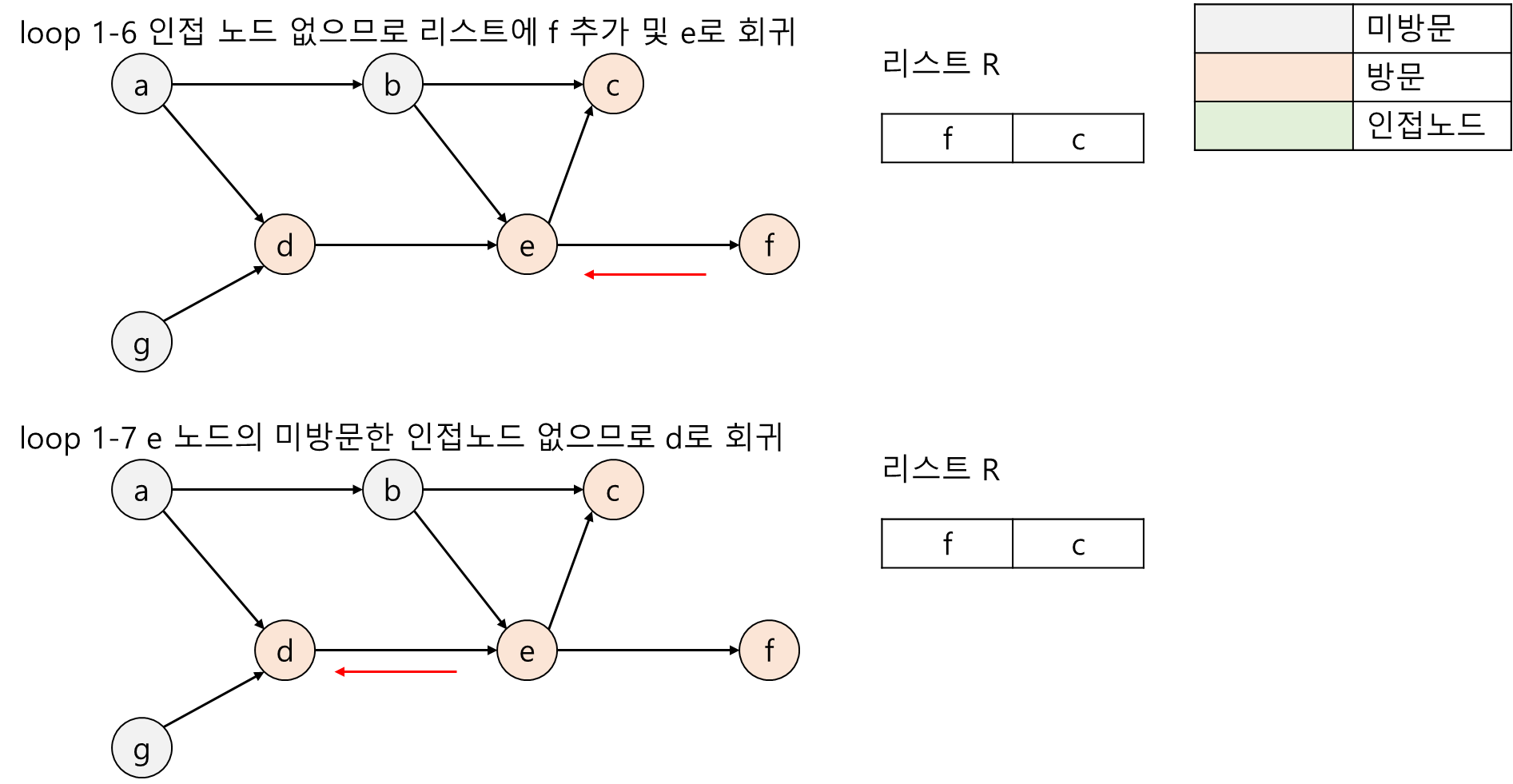
위상 정렬 알고리즘을 구현하는 방법들중 하나는 DFS 순회를 활용하는 방법입니다. DFS 순회는 임의의 노드에서 시작하여 미방문한 인접 노드가 존재하면 순환 호출을 통하여 이동합니다. 그리고 도착한 노드에서 인접 노드가 없는 경우 순환호출 특징 상 되돌아갑니다. 여기서 DFS 순회의 돌아가는 특성을 활용하여 순환 호출에서 돌아갈때 리스트의 앞쪽에 되돌아가기 전 노드를 추가하는 것입니다. 위와 같이 수행하면 리스트에는 작업들의 우선순위가 제일 늦은 순서부터 채워지게 되어 제일 처음 시작한 노드로 회귀할때 리스트에는 위상 정렬된 노드들이 들어있게 됩니다. 이러한 위상 정렬 알고리즘의 시간복잡도는 θ(n+m)입니다.
위상 정렬 알고리즘의 수행과정
- 그래프에서 임의의 미방문한 노드를 선택
- 그 노드를 시작노드로 DFS 순회를 시작
- DFS 순회를 시작하면 노드를 방문 처리하고 그 노드의 인접노드를 탐색함
- 인접 노드중 미방문한 노드가 존재하면 그 인접노드에 대하여 DFS 순회를 순환호출함
- 순회를 수행하다가 더 이상 인접노드가 존재하지 않는다면 그 노드를 리스트 R의 맨 앞에 추가함
- 모든 노드가 방문 될때까지 1~5번 과정을 반복함
- 6번 과정이 끝나면 리스트 R에는 위상 정렬된 노드들이 존재함
아래는 위상 정렬 알고리즘2의 수행과정을 그림으로 표현한것입니다.







6. Java 언어 기반 위상 정렬 알고리즘 구현
@Override
public void topologicalSort() {
boolean[] visited = new boolean[V];
Stack<Integer> stack = new Stack<Integer>();
for(int i=1;i<V;i++)
{
if(!visited[i])
{
topologicalSortUtil(i, visited, stack);
}
}
System.out.print("start");
while(!stack.isEmpty())
{
int nodeNum = stack.pop();
System.out.print("->"+map.get(nodeNum));
}
System.out.println();
}
@Override
public void topologicalSortUtil(int v, boolean[] visited, Stack stack) {
visited[v] = true;
Iterator<Node<E>> itor = adj.get(v).iterator();
while(itor.hasNext())
{
int adjNodeNum = itor.next().getNum();
if(!visited[adjNodeNum])
{
topologicalSortUtil(adjNodeNum, visited, stack);
}
}
stack.push(v);
}public static void main(String[] args)
{
int V = 8;
DirectedGraph<String> directedGraph = new DirectedGraph<String>(V);
Node<String> a = new Node<String>(1, "a");
Node<String> b = new Node<String>(2, "b");
Node<String> c = new Node<String>(3, "c");
Node<String> d = new Node<String>(4, "d");
Node<String> e = new Node<String>(5, "e");
Node<String> f = new Node<String>(6, "f");
Node<String> g = new Node<String>(7, "g");
directedGraph.addEdge(a,b);
directedGraph.addEdge(a,d);
directedGraph.addEdge(b,c);
directedGraph.addEdge(b,e);
directedGraph.addEdge(d,e);
directedGraph.addEdge(e,c);
directedGraph.addEdge(e,f);
directedGraph.addEdge(g,d);
directedGraph.topologicalSort();
}start->g->a->d->b->e->f->c
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph04_topologicalSort
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][Graph] 최소 비용 신장 트리 #2 크루스칼(Kruskal) 알고리즘 개념 및 수행과정 (0) | 2022.01.27 |
|---|---|
| [알고리즘][Graph] 최소 비용 신장 트리 #1 최소 비용 신장 트리의 개념 (0) | 2022.01.26 |
| [알고리즘][Graph] 그래프의 순회 : DFS(Depth-First Search) 개념 및 수행과정 (0) | 2022.01.20 |
| [알고리즘][Graph] 그래프(Graph)의 순회 : BFS(Breadth-First Search) 개념 및 수행과정 (0) | 2022.01.19 |
| [알고리즘][Graph] 그래프(Graph)의 개념과 표현 (0) | 2022.01.18 |