2022. 1. 19. 16:51ㆍAlgorithm
학습목표
1. BFS(Breadth-First Search)가 무엇인지 학습
2. BFS의 수행과정에 대해서 학습
3. BFS와 최단 경로에 대해서 학습
4. BFS의 Java언어 기반 구현
5. BFS의 시간복잡도에 대해서 학습
1. BFS(Breadth-First Search, 너비우선순회)란 무엇인가?
BFS란 그래프를 구성하는 노드들을 순회하는 방법 중에 하나입니다. 여기서 순회란 그래프의 모든 노드들을 방문하는 일을 의미합니다.
BFS 알고리즘은 다음 순서로 노드들을 방문합니다.
- L₀ = {s}, 여기서 s는 출발 노드를 의미함
- L₁ = L₀의 모든 이웃 노드들
- L₂ = L₁의 이웃들 중 L₀에 속하지 않는 노드들
- ...
- L_i = L_(i-1)의 이웃들 중 L_(i-2)에 속하지 않는 노드들

위의 그림을 보면 BFS 순회가 L₀->L₁->L₂->L₃의 순서로써 동심원 형태로 노드들을 방문하는 것을 볼 수 있습니다. 즉, L₀ 동심원에 존재하는 모든 노드들을 방문한 다음 L₁ 동심원에 존재하는 노드를 방문하는 것입니다.
정리하면 BFS 순회란 특정한 노드에서 시작하여 시작 노드를 중심으로 동심원 형태로 인접 노드들을 순회하는 방법을 의미합니다.
2. BFS(너비우선탐색)의 수행 과정
BFS의 수행과정은 다음과 같습니다.
- 시작 노드를 큐에 추가
- 큐에서 노드를 제거
- 제거한 노드를 방문 처리
- 제거한 노드와 인접한 노드들을 큐에 다시 추가
- 2~4번 과정을 큐가 비어 있을 때까지 반복


bfs 순회 시작시 시작노드를 매개변수로 받습니다. 위 그래프에서는 1번 노드에서부터 순회를 시작합니다. 1번 노드가 큐에 들어가면 해당 노드는 방문을 완료한 것입니다.

큐에서 1번 노드를 제거하고 1번 노드와 인접한 노드를 방문처리하고 큐에 추가합니다.
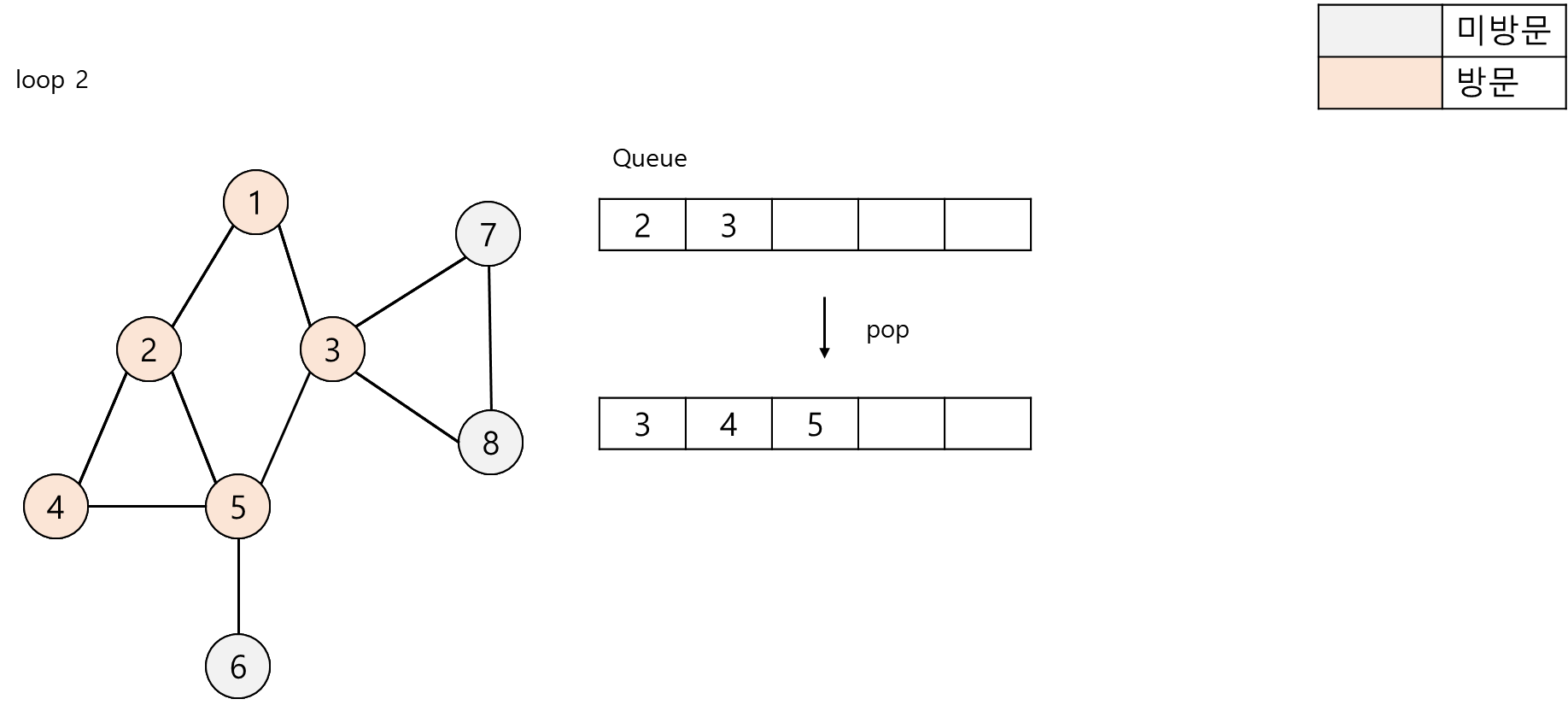
큐에서 2번 노드를 제거하고 2번 노드와 인접한 4,5번 노드를 큐에 추가합니다.

큐에서 3번 노드를 제거하고 3번 노드와 인접한 7,8번 노드를 큐에 추가합니다.
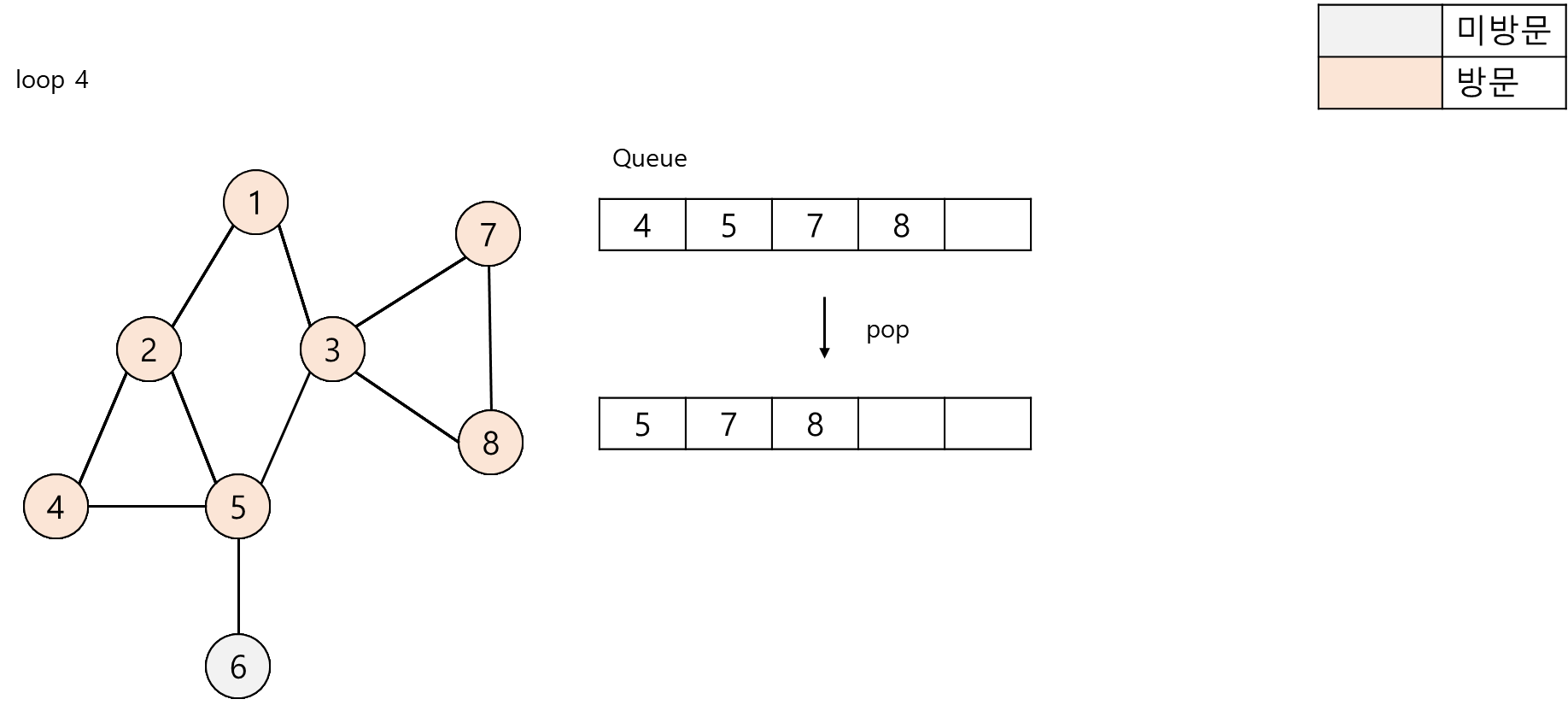
큐에서 4번 노드를 제거하고 4번 노드와 인접한 노드를 탐색합니다. 탐색 결과 5번 노드가 존재하나 5번 노드는 이미 방문한 상태이므로 넘어갑니다.

큐에서 5번 노드를 제거하고 인접한 노드를 탐색합니다. 탐색 결과 6번 노드를 큐에 추가합니다. 그리고 6번 노드를 방문 처리합니다.

7,8,6번 노드는 인접한 노드는 있으나 이미 방문한 노드들밖에 없으므로 큐에서 계속 제거되고 순회를 종료합니다.
3. BFS와 최단경로
아래 그래프에서 노드 s에서 BFS 순회한다고 가정할 때 다음과 같은 사실을 알 수 있습니다.
- s에서 L_i에 속한 노드까지의 최단 경로의 길이는 i이다. (여기서 경로의 길이는 경로에 속한 에지(Edge)의 개수)
- 즉, BFS를 수행하면서 각 노드에 대해서 최단 경로의 길이를 구할 수 있습니다.

예를 들어 시작 노드 s에서 시작하여 L₂영역의 노드까지 가는데 필요한 최단 경로 길이는 2임을 알 수 있습니다.
4. BFS의 Java언어 기반 구현
무방향 그래프 기반의 BFS를 구현합니다.
// 인접리스트 기반 무방향 그래프의 BFS순회
public class UndirectedGraph implements Graph{
private int V; // 노드들의 번호
private ArrayList<ArrayList<Integer>> adj; // 인접리스트
public UndirectedGraph(int v) {
V = v;
adj = new ArrayList<ArrayList<Integer>>(v);
for(int i=0;i<v;i++)
{
adj.add(new ArrayList<Integer>());
}
}
@Override
public void bfsAll() {
boolean[] visited = new boolean[V];
for(int i=0;i<V;i++)
{
if(!visited[i])
{
System.out.printf("%d번 노드에서 시작하는 BFS 순회\n",i);
bfs(i, visited);
System.out.println();
}
}
}
@Override
public void bfs(int s, boolean[] visited) {
LinkedList<Integer> queue = new LinkedList<Integer>();
visited[s] = true;
queue.add(s);
while(queue.size()!=0)
{
s = queue.poll();
System.out.print(s+" ");
Iterator<Integer> itor = adj.get(s).listIterator();
while(itor.hasNext())
{
int adjNode = itor.next();
if(!visited[adjNode])
{
visited[adjNode] = true;
queue.add(adjNode);
}
}
}
}
@Override
public void addEdge(int u, int v) {
adj.get(u).add(v);
adj.get(v).add(u);
}
@Override
public void printGraph()
{
for(int i=0;i<adj.size();i++)
{
System.out.printf("노드 %d의 인접리스트\n", i);
System.out.print("head");
for(int j=0; j<adj.get(i).size();j++)
{
System.out.print("->"+adj.get(i).get(j));
}
System.out.printf("\n\n");
}
}
public static void main(String[] args)
{
int V = 9;
UndirectedGraph undirectedGraph = new UndirectedGraph(V);
undirectedGraph.addEdge(1,2);
undirectedGraph.addEdge(1,3);
undirectedGraph.addEdge(2,3);
undirectedGraph.addEdge(2,4);
undirectedGraph.addEdge(2,5);
undirectedGraph.addEdge(3,5);
undirectedGraph.addEdge(3,7);
undirectedGraph.addEdge(3,8);
undirectedGraph.addEdge(4,5);
undirectedGraph.addEdge(5,6);
undirectedGraph.bfsAll();
}
}0번 노드에서 시작하는 BFS 순회
0
1번 노드에서 시작하는 BFS 순회
1 2 3 4 5 7 8 6
5. BFS의 시간복잡도
인접리스트로 구현할 경우 시간복잡도는 2m이므로 O(n+2m) = O(n+m)이 소요됩니다. 그 이유는 while문을 통해서 모든 노드들이 큐에 추가되었다가 제거되는 과정이 최소 n번이 수행되고, 각각의 노드들에 인접한 노들들을 탐색하는 과정이 2m번 소요되기 때문이다. 이때 노드들에 인접한 다른 노드들은 일정한 개수로 인접하지 않기 때문에 n*2m이 아닌 n+2m이 됩니다. 여기서 m은 무방향 그래프에서는 에지의 개수를 의미하고 2m은 인접리스트에 추가된 노드들의 개수를 입니다. 만약 방향 그래프라면 인접리스트에 존재하는 노드들의 개수는 m이므로 O(n+m)이었을 것입니다.
인접행렬로 구현할 경우 2차원 배열이기 때문에 하나의 노드에 대해서 인접한 노드를 찾기 위해서는 최소 n번이 소요됩니다. n개의 노드*최소 인접 노드 탐색 횟수(n)으로 인하여 O(n²)이 소요될 것입니다.
BFS의 시간복잡도를 정리하면 다음과 같습니다.
- 인접리스트 기반 : O(n+m)
- 인접행렬 기반 : O(n²)
정리하며
그래프의 순회 방법 중 하나인 BFS(Breadth-First Search, 너비우선탐색) 방법은 시작 노드를 중심으로 동심원 형태로 순회하는 방법입니다.
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph02_bfs
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][Graph] DAG(Directed Acyclic Graph)와 위상 정렬(Topological ordering) (0) | 2022.01.25 |
|---|---|
| [알고리즘][Graph] 그래프의 순회 : DFS(Depth-First Search) 개념 및 수행과정 (0) | 2022.01.20 |
| [알고리즘][Graph] 그래프(Graph)의 개념과 표현 (0) | 2022.01.18 |
| [알고리즘][Recursion] 멱집합(Power Set) (0) | 2022.01.17 |
| [알고리즘][Recursion] Counting Cells in a Blob (0) | 2022.01.07 |