[알고리즘][Graph] 그래프의 순회 : DFS(Depth-First Search) 개념 및 수행과정
2022. 1. 20. 13:16ㆍAlgorithm
학습목표
1. DFS은 무엇인지 학습
2. DFS의 수행과정을 학습
3. DFS의 시간복잡도에 대해서 학습
1. DFS(Depth-First Search, 깊이우선탐색)이란 무엇인가?
DFS는 그래프의 순회 방법 중 하나로써 특정 노드에서 시작하여 인접 노드 중 미방문한 노드를 탐색하여 계속해서 이동하는 순회방법을 의미합니다. 이진 트리로 따지면 전위 순회(preorder), 중위 순회(inorder), 후위 순회(postorder)와 비슷합니다.
2. DFS(Depth-First Search, 깊이우선탐색)의 수행과정
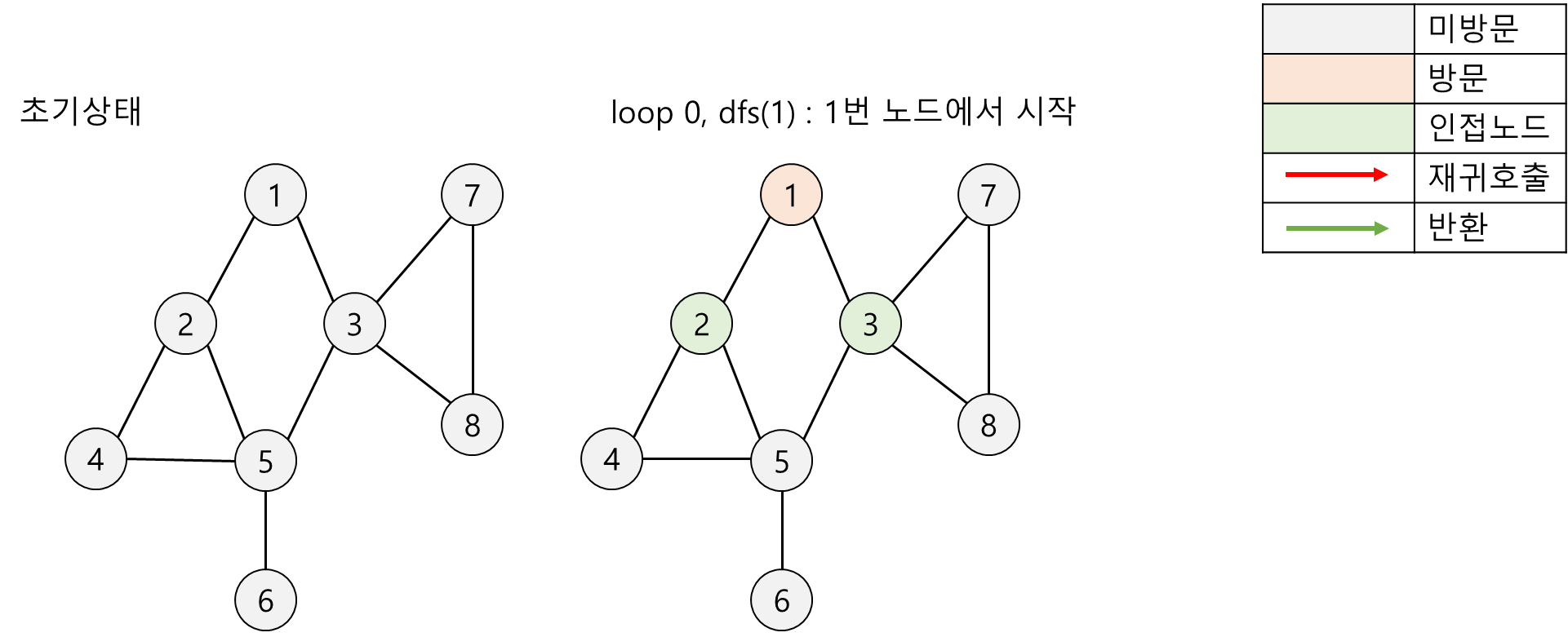
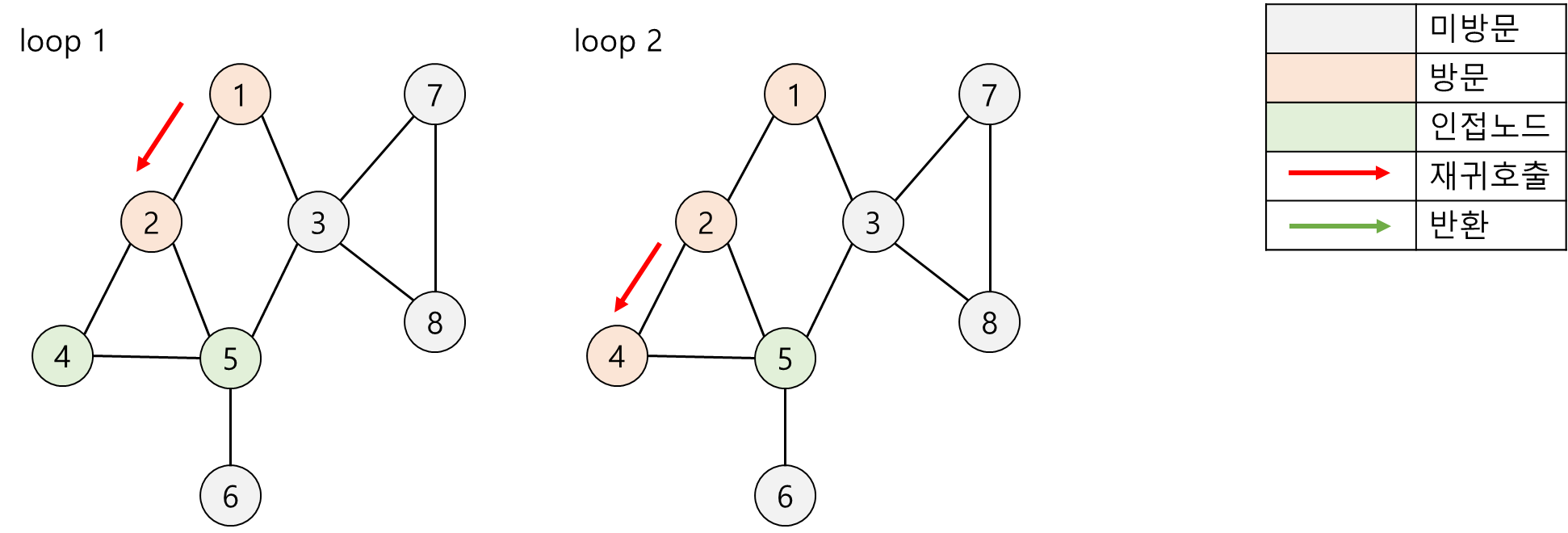
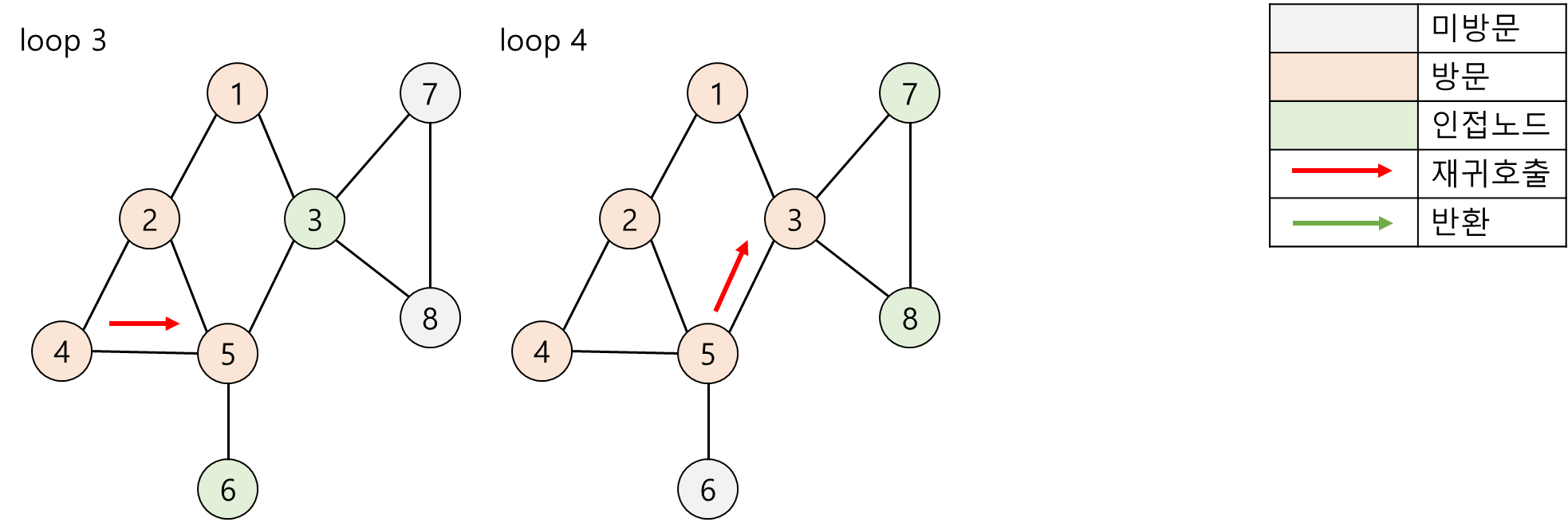

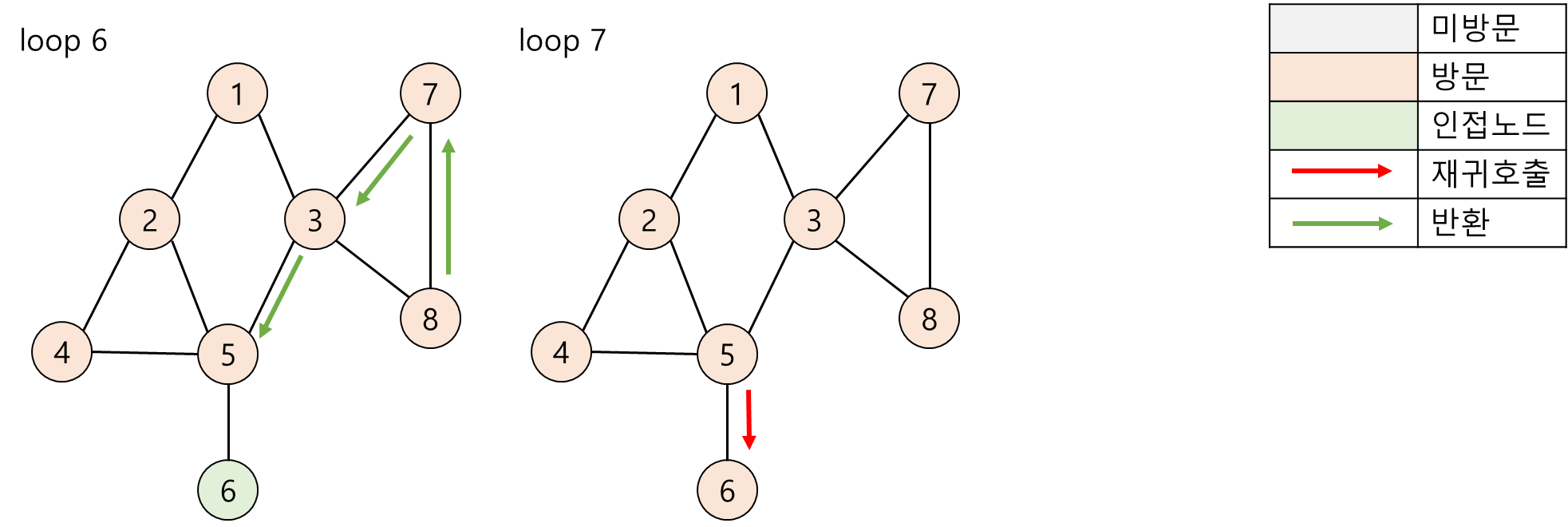

3. Java 언어 기반 DFS 순회 구현
// 인접리스트 기반 무방향 그래프의 BFS순회
public class UndirectedGraph implements Graph{
private int V; // 노드들의 번호
private ArrayList<ArrayList<Integer>> adj; // 인접리스트
public UndirectedGraph(int v) {
V = v;
adj = new ArrayList<ArrayList<Integer>>(v);
for(int i=0;i<v;i++)
{
adj.add(new ArrayList<Integer>());
}
}
@Override
public void dfsAll() {
boolean[] visited = new boolean[V];
for(int i=0;i<V;i++)
{
if(!visited[i])
{
System.out.printf("%d번 노드에서 시작하는 DFS 순회\n",i);
dfs(i,visited);
System.out.println();
}
}
}
@Override
public void dfs(int s, boolean[] visited) {
visited[s] = true;
System.out.print(s+" ");
Iterator<Integer> itor = adj.get(s).iterator();
while(itor.hasNext())
{
int adjNode = itor.next();
if(!visited[adjNode])
{
dfs(adjNode, visited);
}
}
}
@Override
public void bfsAll() {
boolean[] visited = new boolean[V];
for(int i=0;i<V;i++)
{
if(!visited[i])
{
System.out.printf("%d번 노드에서 시작하는 BFS 순회\n",i);
bfs(i, visited);
System.out.println();
}
}
}
@Override
public void bfs(int s, boolean[] visited) {
LinkedList<Integer> queue = new LinkedList<Integer>();
visited[s] = true;
queue.add(s);
while(queue.size()!=0)
{
s = queue.poll();
System.out.print(s+" ");
Iterator<Integer> itor = adj.get(s).listIterator();
while(itor.hasNext())
{
int adjNode = itor.next();
if(!visited[adjNode])
{
visited[adjNode] = true;
queue.add(adjNode);
}
}
}
}
@Override
public void addEdge(int u, int v) {
adj.get(u).add(v);
adj.get(v).add(u);
}
@Override
public void printGraph()
{
for(int i=0;i<adj.size();i++)
{
System.out.printf("노드 %d의 인접리스트\n", i);
System.out.print("head");
for(int j=0; j<adj.get(i).size();j++)
{
System.out.print("->"+adj.get(i).get(j));
}
System.out.printf("\n\n");
}
}
public static void main(String[] args)
{
int V = 9;
UndirectedGraph undirectedGraph = new UndirectedGraph(V);
undirectedGraph.addEdge(1,2);
undirectedGraph.addEdge(1,3);
undirectedGraph.addEdge(2,3);
undirectedGraph.addEdge(2,4);
undirectedGraph.addEdge(2,5);
undirectedGraph.addEdge(3,5);
undirectedGraph.addEdge(3,7);
undirectedGraph.addEdge(3,8);
undirectedGraph.addEdge(4,5);
undirectedGraph.addEdge(5,6);
undirectedGraph.dfsAll();
}
}0번 노드에서 시작하는 DFS 순회
0
1번 노드에서 시작하는 DFS 순회
1 2 3 5 4 6 7 84. DFS 순회의 시간복잡도
- 인접행렬 기반 : O(n²)
- n개의 노드들이 다른 n개의 노드들과 비교하여 방문/미방문을 검사하기 때문에 n개의 노드*n번 방문검사하여 O(n²)이 소요됩니다.
- 인접리스트 기반 : O(n+m)
- n은 노드의 개수를 의미하며 DFS 순회중 무조건 1번은 방문하기 때문에 n번 소요됩니다.
- m은 에지를 의미하며 DFS 순환 호출의 횟수를 의미합니다. 인접 노드에 방문하기 위해서는 에지의 개수만큼 순환호출이 소요됩니다.
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph03_dfs
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][Graph] 최소 비용 신장 트리 #1 최소 비용 신장 트리의 개념 (0) | 2022.01.26 |
|---|---|
| [알고리즘][Graph] DAG(Directed Acyclic Graph)와 위상 정렬(Topological ordering) (0) | 2022.01.25 |
| [알고리즘][Graph] 그래프(Graph)의 순회 : BFS(Breadth-First Search) 개념 및 수행과정 (0) | 2022.01.19 |
| [알고리즘][Graph] 그래프(Graph)의 개념과 표현 (0) | 2022.01.18 |
| [알고리즘][Recursion] 멱집합(Power Set) (0) | 2022.01.17 |