[알고리즘][동적계획법] 동적계획법 #6 Knapsack Problem
2022. 4. 4. 15:37ㆍAlgorithm
학습목표
1. Knapsack Problem에 대하여 학습
2. Knapsack Problem 순환식 정의
3. Java언어 기반 코드 구현
1. Knapsack Problem
Knapsack Problem은 n개의 아이템과 배낭이 존재한다고 가정할때 배낭의 용량을 초과하지 않으면서 아이템의 가격이 최대가 되는 아이템들을 탐색하는 문제입니다. 예를 들어 아래 그림과 같이 아이템의 무게(w)와 가격(v)의 표가 있을 때 배낭에 넣을 수 있고 가격이 최대가 되는 아이템 조합은 3번과 4번 아이템입니다.

2. Knapsack 순환식
- OPT(i, w) : 배낭 용량이 w일 때 아이템 1,2,...,i로 얻을 수 있는 최대 이득
- 경우 1 : 아이템 i를 선택하지 않은 경우
- OPT(i, w) = OPT(i-1, w)
- 경우 2 : 아이템 i를 선택하는 경우
- OPT(i) = v_i + OPT(i-1, w-w_i)
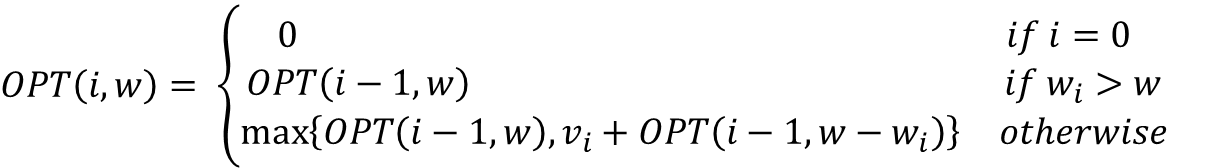
3. Java언어 기반 코드 구현
public class Knapsack {
public static int knapsack(int n, int W, int[] weight, int[] value)
{
int[][] dp = new int[n+1][W+1];
for(int w=0; w<=W; w++)
{
dp[0][w] = 0;
}
for(int i=1; i<=n; i++)
{
for(int w=1; w<=W; w++)
{
if(weight[i]>w)
{
dp[i][w] = dp[i-1][w];
}
else
{
dp[i][w] = Math.max(dp[i-1][w], value[i] + dp[i-1][w-weight[i]]);
}
}
}
print(dp);
return dp[n][W];
}
public static void print(int[][] dp)
{
System.out.println("print dp");
for(int i=0; i<dp.length; i++)
{
for(int j=0; j<dp[i].length; j++)
{
System.out.print(dp[i][j] + "\t");
}
System.out.println();
}
}
public static void main(String[] args)
{
int n = 5;
int W = 11;
int[] weight = {0, 1, 2, 5, 6, 7};
int[] value = {0, 1, 6, 18, 22, 28};
System.out.println(knapsack(n, W, weight, value));
}
}print dp
0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 1 1 1
0 1 6 7 7 7 7 7 7 7 7 7
0 1 6 7 7 18 19 24 25 25 25 25
0 1 6 7 7 18 22 24 28 29 29 40
0 1 6 7 7 18 22 28 29 34 35 40
40
시간복잡도
- O(nW)
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/dp/dp06_knapsack
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][압축] 압축(Compression) #2 Huffman Method with Run-Length Encoding (0) | 2022.04.14 |
|---|---|
| [알고리즘][압축] 압축(Compression) #1 Huffman Coding & Run-Length Encoding (0) | 2022.04.12 |
| [알고리즘][동적계획법] 동적계획법 #5 Longest Common Subsequence (0) | 2022.03.25 |
| [알고리즘][동적계획법] 동적계획법 #4 Matrix-Chain Multiplication (0) | 2022.03.24 |
| [알고리즘][동적계획법] 동적계획법 #3 Optimal Substructure (0) | 2022.03.23 |