[알고리즘][동적계획법] 동적계획법 #5 Longest Common Subsequence
2022. 3. 25. 16:34ㆍAlgorithm
학습목표
1. Longest Common Subsequence가 무엇인지 학습
2. Longest Common Subsequence의 순환식을 정의
3. Longest Common Subsequence의 수행과정을 학습
4. Java언어 기반 Longest Common Subsequence 동적계획법 구현
1. Longest Common Subsequence 문제
- <bcdb>는 문자열 <abcbdab>의 부분수열(Subsequence)입니다.
- <bca>는 문자열 <abcbdab>와 <bdcaba>의 공통 부분수열(Common Subsequence)입니다.
최장 공통 부분수열(Longest Common Subsequence, LCS)은 공통 부분수열(Common Subsequence)들 중 가장 긴 것을 의미합니다. 예를 들어 <bcba>는 <abcbdab>와 <bdcaba>의 LCS입니다.
2. Longest Common Subsequence 순환식 정의
- L[i, j] : 문자열 X = <x1, x2, x3, ... , xi>와 Y = <y1, y2, y3, ..., yj>의 LCS의 길이입니다.
경우 1 : x_i = y_j
- L[i, j] = L[i-1, j-1] + 1
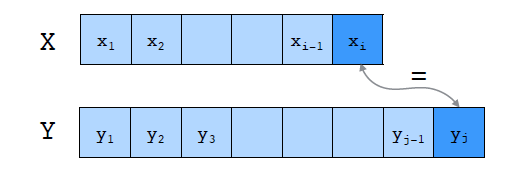
경우 2 : x_i != y_j
- L[i, j] = max( L[i-1, j], L[i, j-1])

경우 3 : i=0 or j=0
- 두 문자열중 한 문자열의 길이가 0이므로 LCS는 0이다.
위 3가지 경우를 정리하면 다음과 같습니다.
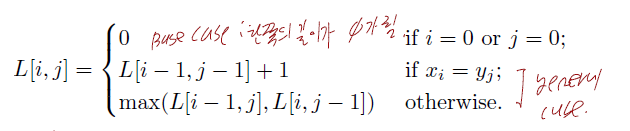
3. Longest Common Subsequence 수행과정
X=ABCBDAB, Y=BDCABA일때의 LCS의 수행과정은 다음과 같습니다.
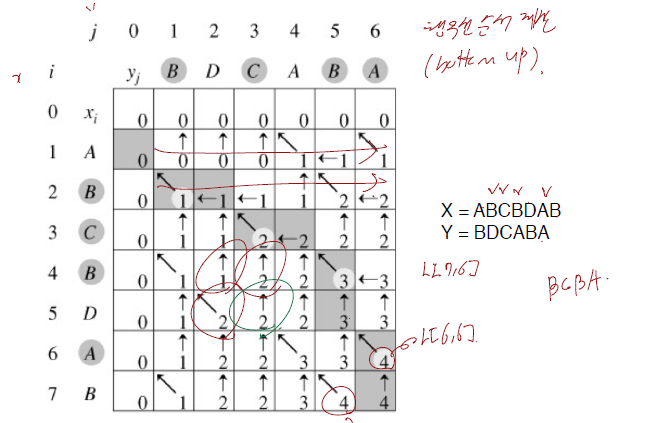
위 그림의 이차원 배열은 Bottom-UP 방식으로 (1,1)부터 (7,6)까지 차례대로 채워질 것입니다. 주목할 점은 예를 들어 ㅣL[7,6]을 계산하기 위해서는 L[6,5], L[6,6], L[7,5]를 먼저 계산해야 합니다. 이는 Bottom-UP 방식으로 저장되기 때문에 자연스럽게 저장되고 계산됩니다.
위 그림에서 최적해인 L[7,6]=4임을 알 수 있고 문자열로 표현하면 <BCBA>입니다.
4. Java언어 기반 Longest Common Subsequence 동적계획법
/**
* @title 가장 긴 공통 부분수열을 구하는 클래스
* - 'bcdb'는 문자열 'abcbdab'의 subsequence이다.
* - 'bca'는 문자열 'abcbdab'와 'bdcaba'의 common subsequence이다.
* - Longest Common Subsequence(LCS) : common subsequence들 중 가장 긴것
* - 'bcba'는 'abcbdab'와 'bdcaba'의 LCS이다.
*/
public class LongestCommonSubsequence {
String x;
String y;
int[][] c;
String[][] z;
/**
* 문자열 x, y의 인덱스는 1부터 시작
* @param x 문자열 x
* @param y 문자열 y
*/
public LongestCommonSubsequence(String x, String y) {
this.x = " "+x;
this.y = " "+y;
c = new int[x.length()+1][y.length()+1];
z = new String[x.length()+1][y.length()+1];
}
/**
* 두 문자열의 LCS(LongestCommonSubsequence)의 길이을 계산합니다.
* @param m 문자열 x의 길이
* @param n 문자열 y의 길이
* @return 두 문자열 x,y의 공통되고 가장 긴 부분수열
*/
public int lcsLength(int m, int n)
{
// 0열 0으로 초기화
for(int i=0; i<=m; i++)
{
c[i][0] = 0;
}
// 0행 0으로 초기화
for(int j=0; j<=n; j++)
{
c[0][j] = 0;
}
// bottom-up 방식으로 계산값 저장됨
// c[i][j] 값을 계산하기 위해서는
// c[i-1][j-1], c[i-1][j], c[i][j-1]가 계산되어야함
for(int i=0; i<=m; i++)
{
for(int j=0; j<=n; j++)
{
// base case
if(i==0 || j==0)
{
continue;
}
// 두 문자의 일치
if(x.charAt(i)==y.charAt(j))
{
c[i][j] = c[i-1][j-1] + 1;
}
// 두 문자의 불일치
else
{
c[i][j] = Math.max(c[i-1][j], c[i][j-1]);
}
}
}
return c[m][n];
}
/**
* 두 문자열의 LCS(LongestCommonSubsequence) 문자열을 계산합니다.
* @param m 문자열 x의 길이
* @param n 문자열 y의 길이
* @return
*/
public String lcsString(int m, int n)
{
// 0열 0으로 초기화
for(int i=0; i<=m; i++)
{
z[i][0] = "";
}
// 0행 0으로 초기화
for(int j=0; j<=n; j++)
{
z[0][j] = "";
}
// bottom-up 방식으로 계산값 저장됨
// c[i][j] 값을 계산하기 위해서는
// c[i-1][j-1], c[i-1][j], c[i][j-1]가 계산되어야함
for(int i=0; i<=m; i++)
{
for(int j=0; j<=n; j++)
{
// base case
if(i==0 || j==0)
{
continue;
}
// 두 문자의 일치
if(x.charAt(i)==y.charAt(j))
{
z[i][j] = z[i-1][j-1] + x.charAt(i);
}
// 두 문자의 불일치
else
{
if(z[i-1][j].length()>z[i][j-1].length())
{
z[i][j] = z[i-1][j];
}
else
{
z[i][j] = z[i][j-1];
}
}
}
}
return z[m][n];
}
}public class Driver {
public static void main(String[] args)
{
String x = "ABCBDAB";
String y = "BDCABA";
LongestCommonSubsequence lcs = new LongestCommonSubsequence(x, y);
System.out.println(lcs.lcsLength(x.length(), y.length()));
}
}Output
4
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/dp/dp05_lcs
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][압축] 압축(Compression) #1 Huffman Coding & Run-Length Encoding (0) | 2022.04.12 |
|---|---|
| [알고리즘][동적계획법] 동적계획법 #6 Knapsack Problem (0) | 2022.04.04 |
| [알고리즘][동적계획법] 동적계획법 #4 Matrix-Chain Multiplication (0) | 2022.03.24 |
| [알고리즘][동적계획법] 동적계획법 #3 Optimal Substructure (0) | 2022.03.23 |
| [알고리즘][BackTracking] N-Queens 문제 (0) | 2022.03.22 |