[알고리즘][동적계획법] 동적계획법 #2 행렬 경로
2022. 3. 4. 15:01ㆍAlgorithm
학습목표
1. 행렬 경로 문제의 순환식 구성
2. 순환식 기반의 Memoization, Dynamic Programming 적용한 메서드 구현
3. 경로 구하기에 대해서 학습
1. 행렬 경로 문제
- 정수들이 저장된 nxn 행렬의 좌상단에서 우하단까지 이동합니다. 단 오른쪽이나 아래쪽 방향으로만 이동할 수 있습니다.
- 방문한 칸에 있는 정수들의 합이 최소화되도록 합니다.
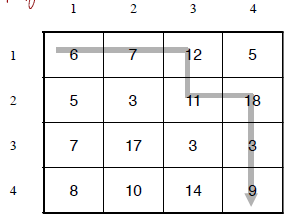
위의 그림에서 (4,4)를 (i, j)라고 할때 (i, j)에 도달하기 위해서는 (i, j-1) 혹은 (i-1, j)를 거쳐야 합니다. 또한 (i, j-1) 혹은 (i-1, j)까지는 최선의 방법으로 이동해야 합니다.
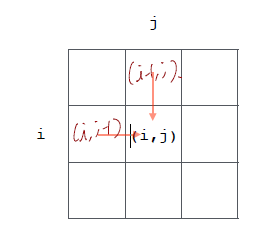
위의 그림을 기반으로 순환식을 구성하면 다음과 같습니다.

재귀적인 알고리즘 구현
public class Driver {
public static int mat(int[][] m, int i, int j)
{
if(i==1 && j==1)
{
return m[i][j];
}
else if(j==1)
{
return mat(m,i-1,j) + m[i][j];
}
else if(i==1)
{
return mat(m,i,j-1) + m[i][j];
}
else
{
return Math.min(mat(m,i-1,j), mat(m,i,j-1)) + m[i][j];
}
}
public static void main(String args[])
{
int[][] m = {{0,0,0,0,0},
{0,6,7,12,5},
{0,5,3,11,18},
{0,7,17,3,3},
{0,8,10,14,9}
};
System.out.println(mat(m,4,4));
}
}
2. 행렬 경로 : Memoization
public class Driver {
static int[][] dp = new int[5][5];
public static int mat(int[][] m, int i, int j)
{
if(dp[i][j]!=0)
{
return dp[i][j];
}
if(i==1 && j==1)
{
dp[i][j] = m[i][j];
}
else if(j==1)
{
dp[i][j] = mat(m,i-1,j) + m[i][j];
}
else if(i==1)
{
dp[i][j] = mat(m,i,j-1) + m[i][j];
}
else
{
dp[i][j] = Math.min(mat(m,i-1,j), mat(m,i,j-1)) + m[i][j];
}
return dp[i][j];
}
public static void main(String args[])
{
int[][] m = {{0,0,0,0,0},
{0,6,7,12,5},
{0,5,3,11,18},
{0,7,17,3,3},
{0,8,10,14,9}
};
System.out.println(mat(m,4,4));
}
}
3. 행렬 경로 및 경로 출력 : 동적 계획법
public class Driver {
static int[][] dp = new int[5][5];
static char[][] path = new char[5][5];
public static int mat(int[][] m, int n)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==1 && j==1)
{
dp[i][j] = m[i][j];
path[i][j] = '-';
}
else
{
if(dp[i-1][j]<dp[i][j-1]) // 위쪽
{
dp[i][j] = m[i][j] + dp[i-1][j];
path[i][j] = '↑';
}
else // 왼쪽
{
dp[i][j] = m[i][j] + dp[i][j-1];
path[i][j] = '←';
}
}
}
}
return dp[n][n];
}
public static void printPath(char[][] path, int i, int j)
{
while(path[i][j]!='-')
{
System.out.print(i + " " + j+"\n");
if(path[i][j]=='←')
{
j--;
}
else
{
i--;
}
}
System.out.print(i + " " + j+"\n");
}
public static void printPathRecursive(char[][] path, int i, int j)
{
if(path[i][j]=='-')
{
System.out.print(i + " " + j + "\n");
}
else
{
if(path[i][j]=='↑')
{
printPathRecursive(path, i-1, j);
}
else if(path[i][j]=='←')
{
printPathRecursive(path, i, j-1);
}
System.out.print(i + " " + j + "\n");
}
}
public static void main(String args[])
{
int[][] m = {{0,0,0,0,0},
{0,6,7,12,5},
{0,5,3,11,18},
{0,7,17,3,3},
{0,8,10,14,9}
};
int n = 4;
for(int i=0;i<=n;i++)
{
dp[i][0] = Integer.MAX_VALUE;
}
for(int j=0;j<=n;j++)
{
dp[0][j] = Integer.MAX_VALUE;
}
System.out.println(mat(m,4));
//printPath(path, n, n);
printPathRecursive(path, n, n);
}
}
References
Source Code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/dp/dp03_matrix_path
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][동적계획법] 동적계획법 #3 Optimal Substructure (0) | 2022.03.23 |
|---|---|
| [알고리즘][BackTracking] N-Queens 문제 (0) | 2022.03.22 |
| [알고리즘][동적계획법] 동적계획법 #1 피보나치 수, 이항계수 (0) | 2022.03.03 |
| [알고리즘][Graph] 최단 경로(Shortest Path) #3 최단 경로 문제, Floyd-Warshall 알고리즘 (0) | 2022.02.25 |
| [알고리즘][Graph] 최단 경로(Shortest Path) #2 최단 경로 문제, Dijkstra 알고리즘 (0) | 2022.02.22 |