2022. 3. 3. 14:45ㆍAlgorithm
학습목표
1. 일반적인 피보나치수 재귀 메서드의 중복계산을 개선
2. 일반적인 이항게수 재귀 메서드의 중복계산을 개선
3. Memoization과 Dynamic Programming의 특징에 대해서 학습
1. 피보나치 수(Fibonacci Numbers)
피보나치 수란 0번째 및 1번째 항이 0과 1이며 그 뒤의 모든 항은 바로 앞 두항의 합인 수열입니다.
0 1 1 2 3 5 8 13 ...피보나치 수의 점화식은 다음과 같습니다.
f(0) = 0
f(1) = 1
f(n) = f(n-1) + f(n-2), if n>=2
위의 점화식을 기반으로 피보나치 수의 재귀적인 메서드를 구현하면 다음과 같습니다.
public class Driver {
public static int fibo(int n)
{
if(n<2)
{
return n;
}
return fibo(n-1) + fibo(n-2);
}
public static void main(String args[])
{
System.out.println(fibo(7)); // 13
}
}13위의 결과를 통해서 7번째 항의 피보나치 수가 13인 것을 알 수 있습니다. 그러나 위의 fibo 메서드는 문제점이 존재합니다. 문제점은 fibo(7)을 계산하기 위해서 fibo(6)과 fibo(5)를 재귀적으로 호출하였을 것이고 fibo(6)과 fibo(5) 또한 다시 재귀적으로 밑의 항들을 호출하였을 것입니다. 이는 중복된 계산이 발생합니다. 그림으로 표현하면 다음과 같습니다.

2. 피보나치 수 : Memoization
Memoization 기술이란 무엇인가?
Memoization 기술은 특정 저장 장소(배열 등)에 계산한 결과를 저장하고 활용하는 기술입니다. 예를 들어 fibo(7)를 호출하면 fibo(5)를 호출하는 과정에서 fibo(1) ~fibo(4)까지 계산을 한번씩만 수행하고 Memoizatio 저장소에 저장하는 것입니다. 그리고 fibo(6)을 호출하는 과정에서 fibo(1)~fibo(5)까지 이미 계산되어 있으므로 fibo(6)은 저장소에서 이미 계산된 결과를 가져오기만 하면 되는 것입니다.
위의 설명을 기반으로 피보나치 수에 Memoization 기술을 적용하면 다음과 같습니다.
public class Driver {
static int[] dp = new int[100];
public static int fibo(int n)
{
if(n<2)
{
return n;
}
else if(dp[n]!=0)
{
return dp[n];
}
else
{
dp[n] = fibo(n-1) + fibo(n-2);
return dp[n];
}
}
public static void main(String[] args) {
System.out.println(fibo(7));
}
}13위의 예제에서 dp 정수형 배열이 Memoization의 저장소입니다. 초기화는 0으로 되어있기 때문에 dp[n]=0이라면 아직 계산하기 이전이므로 재귀적인 호출을 수행하고 dp[n]!=0이라면 이미 계산된 항이므로 dp[n]을 반환하면 됩니다.
2. 피보나치 수 : Dynamic Promgramming
중복된 계산을 피하기 위해서 피보나치 수 메서드를 재귀적으로 호출하는 것이 아닌 반복문을 통해서 0번째부터 순차적으로 계산하고 저장할 수 있습니다. 이러한 방식을 bottom-up 방식이라고 합니다.
피보나치 수를 bottom-up 방식을 적용하면 다음과 같습니다.
public class Driver {
public static int fibo(int n)
{
int[] dp = new int[n+1];
dp[0] = 0;
dp[1] = 1;
for(int i=2;i<=n;i++)
{
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
public static void main(String[] args) {
System.out.println(fibo(7));
}
}dp 배열의 0번째부터 순차적으로 채워지기 때문에 중복된 계산을 하지 않습니다.
4. 이항 계수(Binomial Coefficient)
이항 계수란 주어진 크기 집합(n)에서 원하는 개수(k)만큼 순서 없이 뽑는 조합의 가짓수를 의미합니다. 예를 들어 n=3, k=2이라면 3가지중에서 2가지를 뽑는 경우의 수를 의미합니다.
1,2,3
n=3, k=2
(1,2,3)중에서 순서없이 2가지를 뽑는 경우의 수
=> (1,2), (1,3), (2,3)
=> 총 3가지
이항 계수의 점화식은 다음과 같습니다.
(n,k) = 1, if n=k or k=0
(n,k) = (n-1,k) + (n-1,k-1), otherwise
위 점화식을 기반으로 재귀적인 이항계수 메서드를 구현하면 다음과 같습니다.
public class Driver {
public static int binomial(int n, int k)
{
if(n==k || k==0)
{
return 1;
}
return binomial(n-1,k) + binomial(n-1,k-1);
}
public static void main(String[] args) {
System.out.println(binomial(5,2)); // 10
}
}위의 예제를 통하여 binomial 재귀 메서드역시 피보나치 수처럼 호출 과정에서 중복된 계산이 발생하는 것을 알 수 있습니다. 중복된 계산을 해결하기 위해서 마찬가지로 Memoization 기술이나 Bottom-Up 방식으로 문제를 해결할 수 있습니다.
5. 이항 계수(Binomial Coefficient) : Memoization
Memoization 기술을 적용하기 전에 n과 k에 따른 이항 계수 값을 표로 그리면 다음과 같습니다.
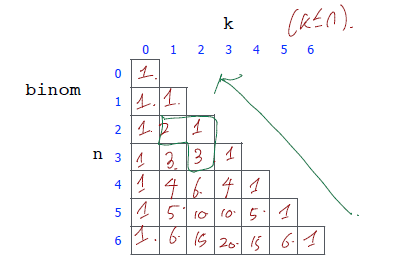
위의 그림을 통하여 binomial이라는 이차원 배열 저장소에 계산된 결과를 저장하면 됩니다.
이항 계수 재귀 메서드에 Memoization 기술을 적용하면 다음과 같습니다.
public class Driver {
static int[][] binomial = new int[100][100];
public static int binomial(int n, int k)
{
if(n==k || k==0)
{
return 1;
}
else if(binomial[n][k]!=0)
{
return binomial[n][k];
}
binomial[n][k] = binomial(n-1,k) + binomial(n-1,k-1);
return binomial[n][k];
}
public static void main(String[] args) {
System.out.println(binomial(5,2));
}
}
6. 이항 계수(Binomial Coefficient) : Dynamic Programming
중복된 계산을 피하기 위해서 재귀적인 호출을 사용하지 않고 반복문을 통하여 binomial 배열을 (0,0)부터 채워나가서 (n,k)까지 채워나갑니다.
public class Driver {
static int[][] binomial = new int[100][100];
public static int binomial(int n, int k)
{
for(int i=0; i<=n; i++)
{
for(int j=0; j<=k && j<=i; j++)
{
if(i==j || j==0)
{
binomial[i][j] = 1;
}
else
{
binomial[i][j] = binomial(i-1,j) + binomial(i-1, j-1);
}
}
}
return binomial[n][k];
}
public static void main(String[] args) {
System.out.println(binomial(5,2));
}
}
7. Memoization vs Dynamic Programming
- 순환식의 값을 계산하는 기법들입니다.
- 둘 다 동적 계획법의 일종으로 보기도 합니다.
- Memoization은 top-down 방식이며, 실제로 필요한 부분문제(subproblem)만을 계산합니다.
- 동적 계획법은 bottom-up 방식이며, 재귀에 수반되는 overhead가 없습니다.
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/dp
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][BackTracking] N-Queens 문제 (0) | 2022.03.22 |
|---|---|
| [알고리즘][동적계획법] 동적계획법 #2 행렬 경로 (0) | 2022.03.04 |
| [알고리즘][Graph] 최단 경로(Shortest Path) #3 최단 경로 문제, Floyd-Warshall 알고리즘 (0) | 2022.02.25 |
| [알고리즘][Graph] 최단 경로(Shortest Path) #2 최단 경로 문제, Dijkstra 알고리즘 (0) | 2022.02.22 |
| [알고리즘][Graph] 최단 경로(Shortest Path) #1 최단 경로 문제, Bellman-Ford 알고리즘 (0) | 2022.02.21 |