2022. 2. 25. 17:30ㆍAlgorithm
학습목표
1. Floyd-Warshall 알고리즘이 무엇인지 학습
2. Floyd-Warshall 알고리즘 수행과정에 대해서 학습
3. Java 언어 기반 Floyd-Warshall 알고리즘 구현
1. Floyd-Warshall 알고리즘이란 무엇인가?
이전글에서 작성한 Bellman-Ford, Dijkstra 알고리즘은 Single-Source 문제의 유형으로 임의의 한 노드에서 다른 모든 노드까지의 최단 경로를 계산하는 알고리즘이였습니다. Floyd-Warshall 알고리즘은 All-Paris 문제의 유형으로 모든 정점에서 다른 모든 정점으로의 최단 경로를 계산하는 알고리즘입니다. 즉, Floyd-Warshall 알고리즘은 모든 노드의 순서쌍에 대해서 최단 경로를 계산하는 알고리즘입니다.
예를 들어 인접행렬 기반 방향 가중치 그래프의 입력이 다음과 같을때 최단 경로는 다음과 같습니다.
Input
int[][] graph = { { 0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
}
위와 같은 그래프가 존재한다고 할때 각각의 정점이 다른 정점으로 가는 비용을 계산하면 아래와 같습니다.

위의 표에서 INF의 의미는 무한대를 의미하며, 임의의 노드가 해당 노드로 갈수 없다는 것을 의미합니다. 예를 들어 graph[1][0]은 방향 간선이 없기 때문에 최단 경로를 계산할 수 없어 INF로 저장됩니다.
2. Floyd-Warshall 알고리즘
Floyd-Warshall 알고리즘은 동적 계획법에 의거하여 수행됩니다. 어떤 노드의 순서쌍 (i,j)가 있다고 가정하면 dist[i][j]의 의미는 노드 i에서 출발하여 여러 노드를 거쳐서 노드 j에 도착하였을때 최단 경로 값을 의미합니다. 이때 노드 i에서 노드 j를 거칠때 중간 노드들을 거칩니다. 이 중간 노드들을 k로 정의합니다. dist[i][j]의 후보로 나올 수 있는 경우는 다음과 같습니다.
- k를 거치지 않는 경우 : {1, 2, ..., k-1} 사이에 노드를 거쳐서 노드 i에서 노드 j에 도착하는 경로들 중 최소 경로인 값
- k를 거치는 경우 : {1, 2, ..., k-1} 사이에 노드들을 거쳐서 노드 i에서 노드 k에 도착하는 경로들 중 최소 경로인 값 + {1, 2, ..., k-1} 사이에 노드들을 거쳐서 노드 k에서 노드 j에 도착하는 경로들 중 최소 경로인 값
위의 경우를 점화식으로 세우면 다음과 같습니다.
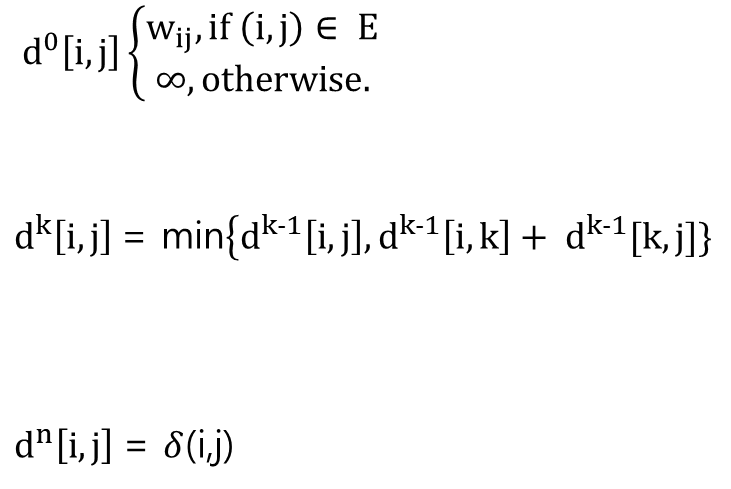
3. Java 기반 Floyd-Warshall 알고리즘 구현
public void floydWarshall()
{
int[][] dist = new int[V][V];
int[][] pi = new int[V][V];
for(int i=0;i<V;i++)
{
for(int j=0;j<V;j++)
{
dist[i][j] = weight[i][j];
pi[i][j] = -1;
}
}
for(int k=0;k<V;k++)
{
for(int i=0;i<V;i++)
{
for(int j=0;j<V;j++)
{
if(dist[i][j] > dist[i][k] + dist[k][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
pi[i][j] = k;
}
}
}
}
printDistancePath(dist);
}public class Driver {
public static void main(String[] args)
{
int V = 4, E = 4;
DirectedGraph<String> directedGraph = new DirectedGraph<String>(V,E);
Node<String> s = new Node<String>(0, "s");
Node<String> t = new Node<String>(1, "t");
Node<String> x = new Node<String>(2, "x");
Node<String> y = new Node<String>(3, "y");
directedGraph.addEdge(s, t, 5);
directedGraph.addEdge(s, y, 10);
directedGraph.addEdge(t, x, 3);
directedGraph.addEdge(x, y, 1);
// directedGraph.printGraph();
directedGraph.floydWarshall();
}
}0 5 8 9
INF 0 3 4
INF INF 0 1
INF INF INF 0
References
Source Code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph12_floydwarshall_shortestpath
GeeksForGeeks : https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp-16/
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][동적계획법] 동적계획법 #2 행렬 경로 (0) | 2022.03.04 |
|---|---|
| [알고리즘][동적계획법] 동적계획법 #1 피보나치 수, 이항계수 (0) | 2022.03.03 |
| [알고리즘][Graph] 최단 경로(Shortest Path) #2 최단 경로 문제, Dijkstra 알고리즘 (0) | 2022.02.22 |
| [알고리즘][Graph] 최단 경로(Shortest Path) #1 최단 경로 문제, Bellman-Ford 알고리즘 (0) | 2022.02.21 |
| [알고리즘][Graph] 최소 비용 신장 트리 #4 프림(Prim's) 알고리즘의 개념과 수행과정 (0) | 2022.02.15 |