2022. 2. 15. 17:40ㆍAlgorithm
학습목표
1. 프림(Prim's) 알고리즘이란 무엇인지 학습
2. 프림 알고리즘의 수행과정에 대해서 학습
3. Java언어 기반 프림 알고리즘 구현을 수행
3. 프림 알고리즘의 시간복잡도에 대해서 학습
1. 프림(Prim's) 알고리즘이란 무엇인가?
프림 알고리즘은 최소 비용 신장 트리(Minimum Spanning Tree, MST)를 탐색하기 위해 사용되는 알고리즘입니다. 프림 알고리즘은 임의의 노드에서 시작하여 출발 노드를 포함하는 트리(MST)를 점점 키워갑니다. 그리고 매 단계에서 이미 트리에 포함된 노드와 포함되지 않은 노드를 연결하는 간선들 중 가장 가중치가 작은 에지를 선택하는 알고리즘입니다.
2. 프림(Prim's) 알고리즘의 수행과정
프림 알고리즘의 수행과정은 다음과 같습니다.
- 그래프의 노드중 임의의 노드(start)에서 출발
- key[start] = 0 저장
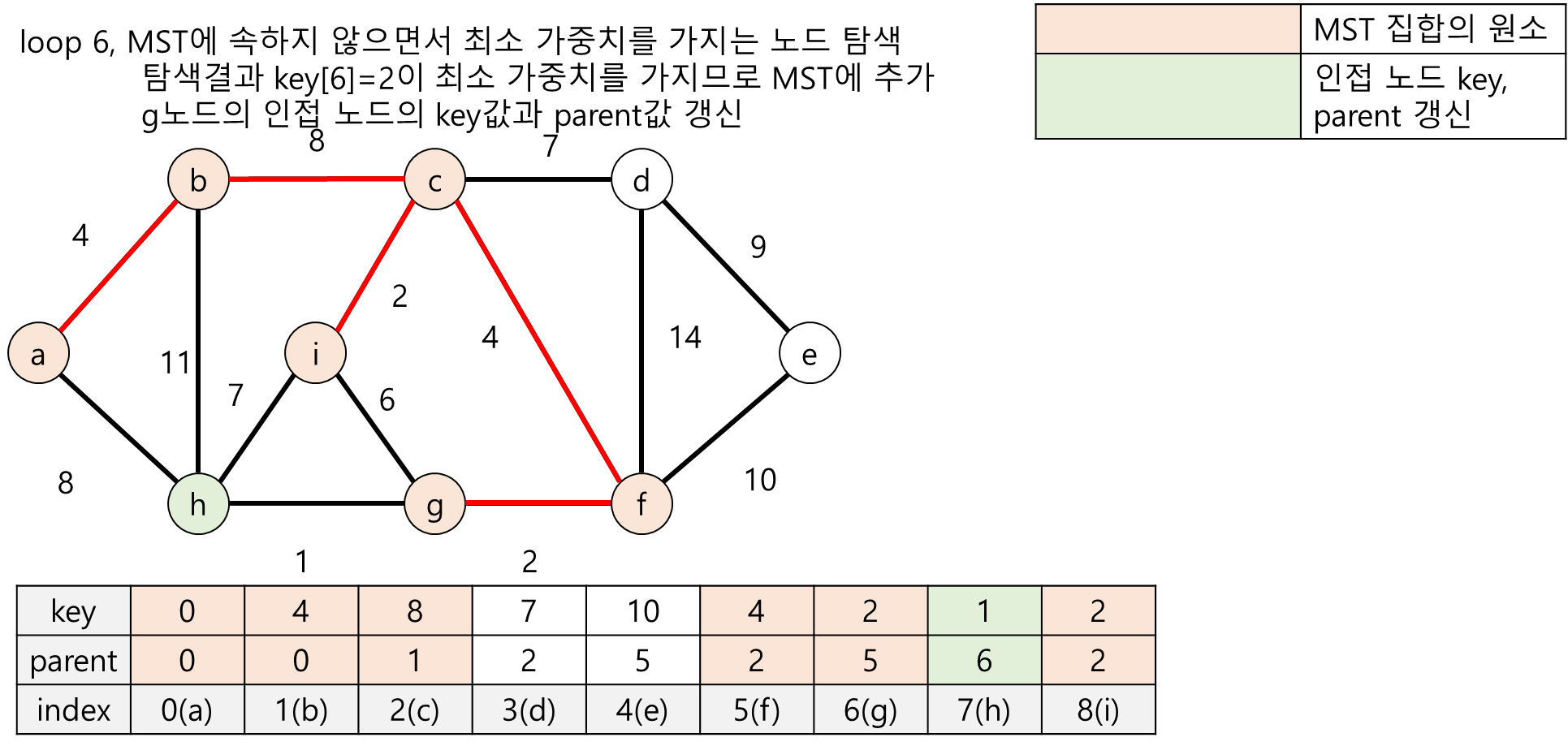
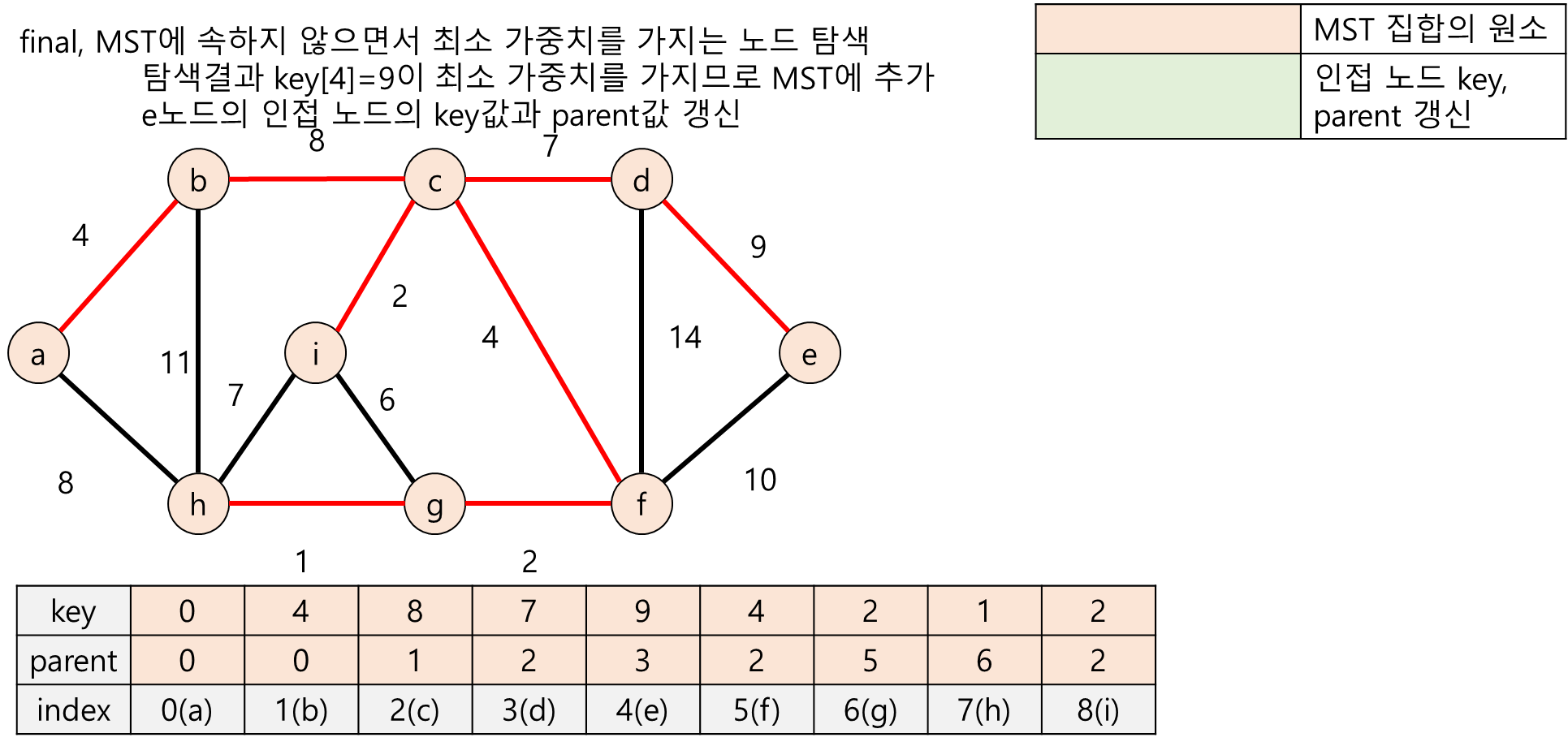
- key 배열을 탐색하여 MST 트리에 포함되지 않으면서 key값이 최소인 노드 u를 탐색함
- key값이 최소인 노드 u를 MST 트리에 추가함 (합집합)
- 노드 u와 인접하고 MST 트리에 포함되지 않는 노드들 v의 key값과 parent값을 갱신함
- 위와 같은 노드 v와 이루는 간선들중 가중치가 가장 작은 값으로 key값을 갱신
- 가중치가 가장 작은 간선 (u,v)에서 parent[v] = u로 설정함
- MST 집합의 개수가 n개가 될때까지 2~4번 과정을 반복합니다.
아래 그림과 같이 무방향 가중치 그래프가 존재한다고 가정합니다.
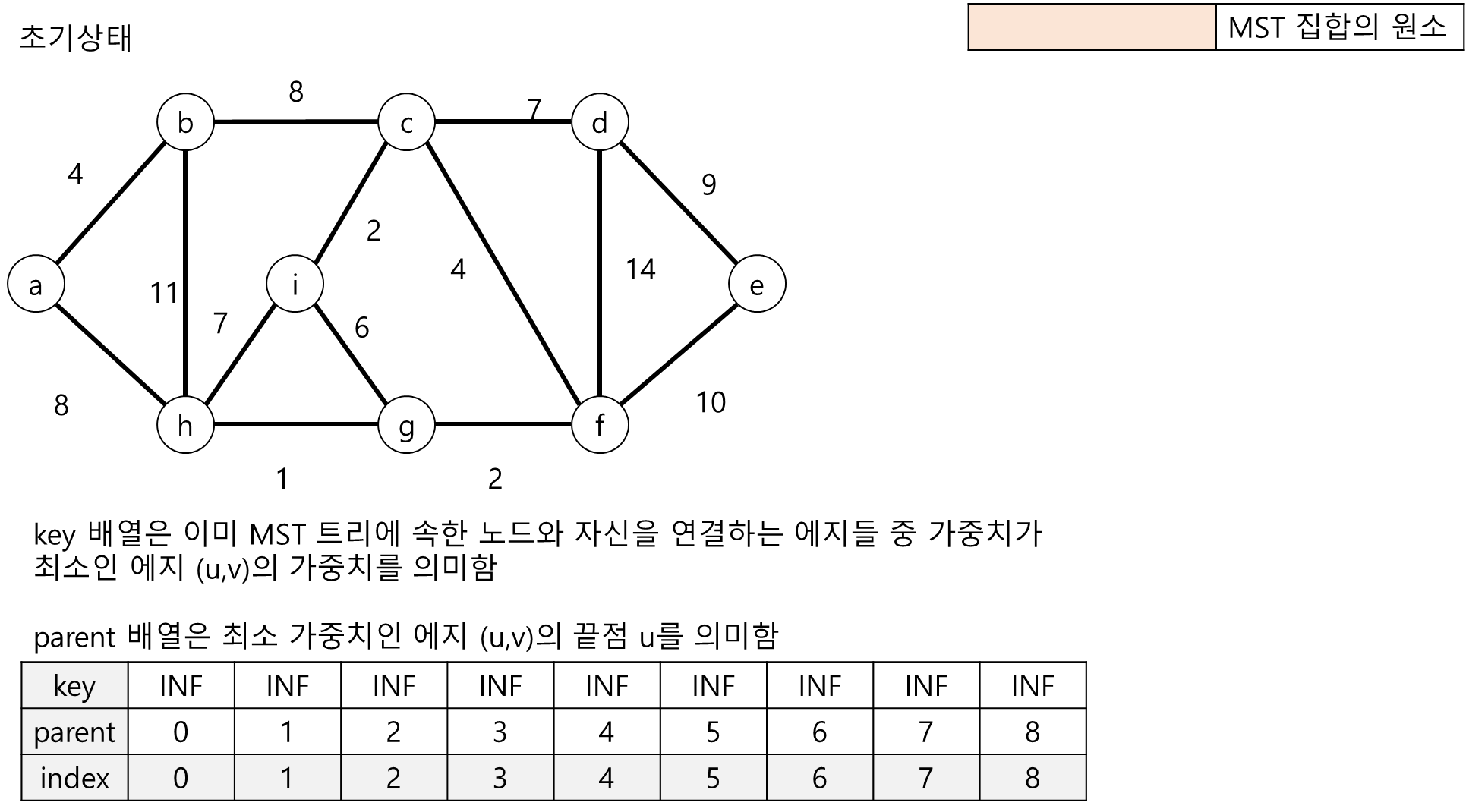
- 노드 a~i : 정수 0~8로 대응
- key : MST 트리에 속한 노드와 자신을 연결하는 간선들 중 가중치가 최소인 에지 (u,v)의 가중치를 저장함
- parent : 최소 가중치 간선 (u,v)에서 u를 저장함, 예를 들어서 parent[1] = 0 이라면 노드 b와 연결된 노드는 a라는 의미
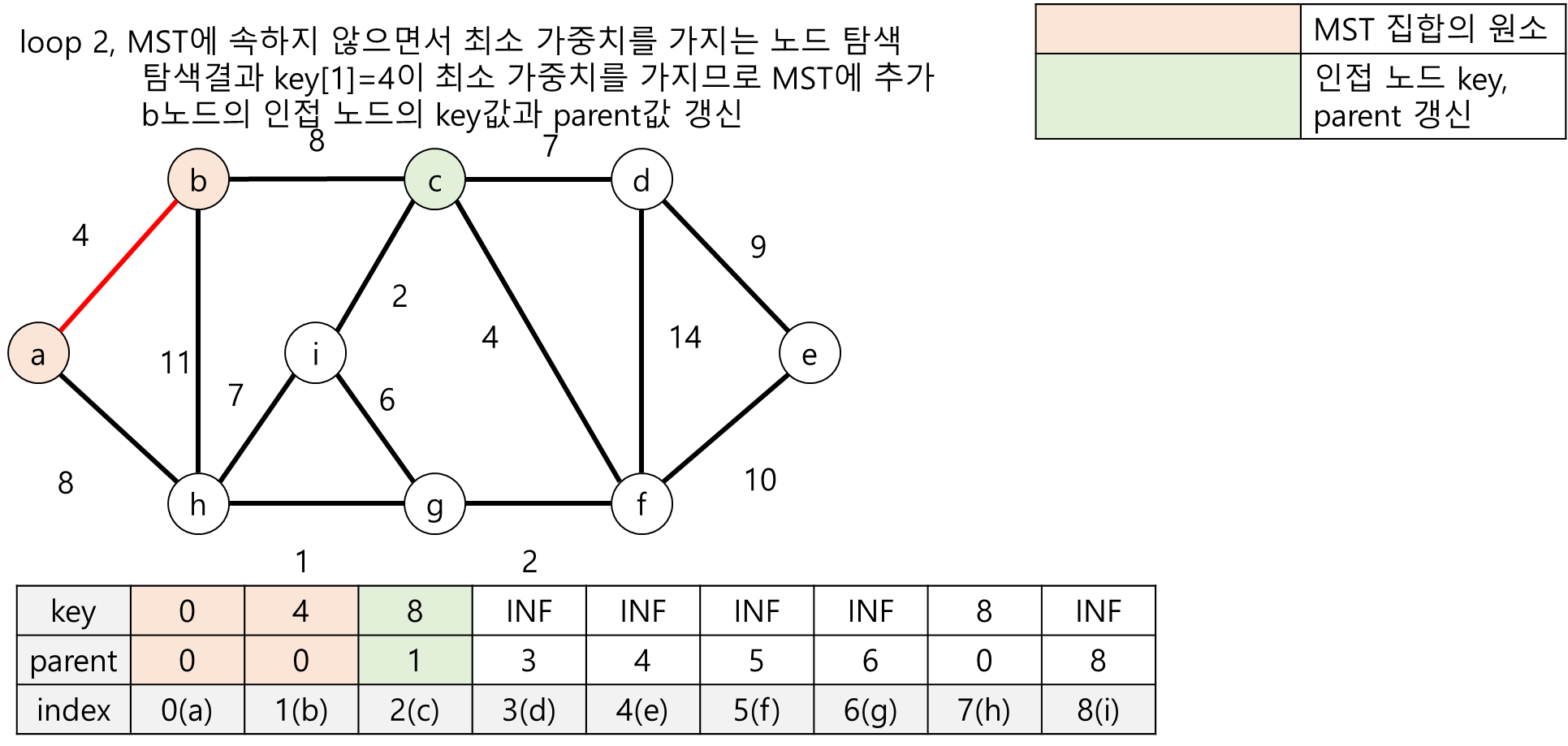
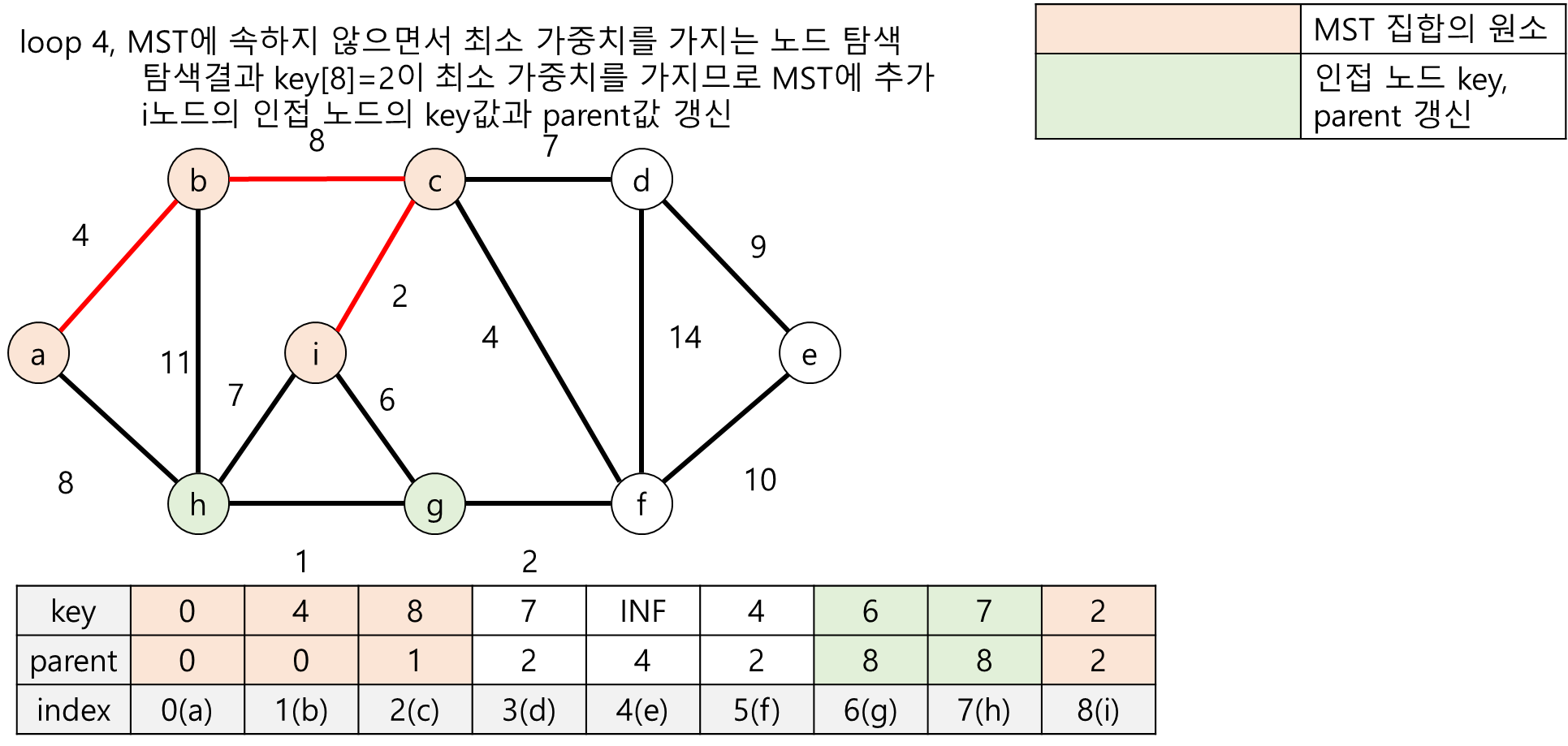
다음 그림들은 프림 알고리즘의 수행과정을 그림으로 표현한 것입니다.






3. Java언어 기반 프림 알고리즘 구현 O(n²)
public void primMST(int start)
{
// MST 트리에 속한 노드와 자신을 연결하는 간선들 중
// 가중치가 최소인 간선 (u,v)의 가중치를 의미함.
int[] key = new int[V];
// 최소 가중치인 간선 (u,v)의 끝점 u를 의미함.
int[] parent = new int[V];
// 모든 노드의 key값과 parent값을 초기화
for(int u=0; u<V; u++)
{
key[u] = Integer.MAX_VALUE;
parent[u] = u;
}
// MST 집합에 포함된 노드들
ArrayList<Node<E>> nodes = new ArrayList<Node<E>>();
// start 노드에서부터 시작함
// 시작 노드는 가중치가 없기 때문에 0으로 설정함
key[start] = 0;
int v = 0;
while(nodes.size()<V) // MST 집합의 개수가 V-1개가 될때까지 반복함
{
// MST 집합에 속하지 않으면서 최소 가중치를 가지는 노드 탐색
int u = findMinKey(nodes,key);
// MST 집합에 추가
nodes.add(map.get(u));
// u의 인접노드의 key값과 parent값 갱신
for(Node<E> node : adj.get(u))
{
v = node.num;
// 인접 노드 v에서 MST 집합에 포함되지 않으면서 간선 가중치가 가장 작은 것으로 갱신
if(key[v] > edges[u][v] && !nodes.contains(map.get(v)))
{
key[v] = edges[u][v];
parent[v] = u;
}
}
}
// MST 결과 출력
printMST(key, parent);
}
public int findMinKey(ArrayList<Node<E>> nodes, int[] key)
{
int min_idx = 0; // 최소 가중치를 가지는 노드 인덱스
int min_val = Integer.MAX_VALUE; // 최소 가중치 값
for(int i=0;i<V;i++)
{
if(key[i]<min_val && !nodes.contains(map.get(i)))
{
min_idx = i;
min_val = key[i];
}
}
return min_idx;
}위 알고리즘은 프림 알고리즘의 핵심 메서드입니다. 전체 소스코드는 아래의 링크를 통해 확인할 수 있습니다.
https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph09_prim_mst
GitHub - yonghwankim-dev/inflearn_algorithm: [인강] 자바 언어 기반 영리한 프로그래밍을 위한 알고리즘 강
[인강] 자바 언어 기반 영리한 프로그래밍을 위한 알고리즘 강좌. Contribute to yonghwankim-dev/inflearn_algorithm development by creating an account on GitHub.
github.com
public class Driver {
public static void main(String[] args) {
UndirectedGraph<String> graph = new UndirectedGraph<String>(9);
Node<String> a = new Node<String>(0, "a");
Node<String> b = new Node<String>(1, "b");
Node<String> c = new Node<String>(2, "c");
Node<String> d = new Node<String>(3, "d");
Node<String> e = new Node<String>(4, "e");
Node<String> f = new Node<String>(5, "f");
Node<String> g = new Node<String>(6, "g");
Node<String> h = new Node<String>(7, "h");
Node<String> i = new Node<String>(8, "i");
graph.addEdge(a, b, 4);
graph.addEdge(a, h, 8);
graph.addEdge(b, c, 8);
graph.addEdge(b, h, 11);
graph.addEdge(c, d, 7);
graph.addEdge(c, i, 2);
graph.addEdge(c, f, 4);
graph.addEdge(d, f, 14);
graph.addEdge(d, e, 9);
graph.addEdge(e, f, 10);
graph.addEdge(f, g, 2);
graph.addEdge(g, i, 6);
graph.addEdge(g, h, 1);
graph.addEdge(h, i, 7);
//graph.printGraph();
graph.primMST(0);
}
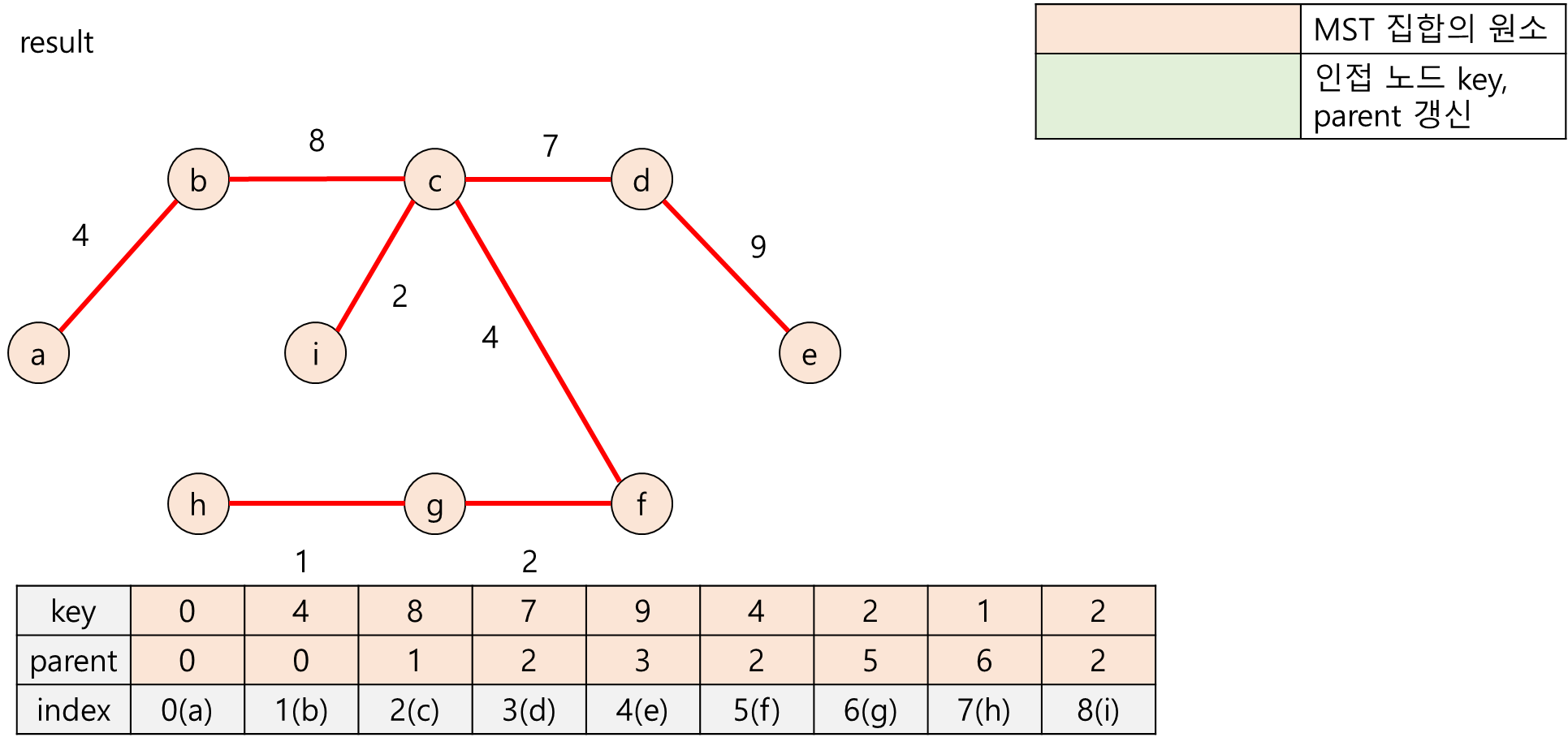
}key : [0, 4, 8, 7, 9, 4, 2, 1, 2]
parent : [0, 0, 1, 2, 3, 2, 5, 6, 2]
MST Edges
a - b 4
b - c 8
c - d 7
d - e 9
c - f 4
f - g 2
g - h 1
c - i 2
4. 프림 알고리즘 시간복잡도
n이 그래프의 노드 개수라고 가정한다면 위에서 구현한 프림 알고리즘의 시간복잡도는 다음과 같습니다.
- key, parent 초기화 : O(n)
- while문 : O(n)
- key 최소값 탐색 : O(n)
- 인접노드의 key, parent 값 갱신 : degree(u) = O(n)
while문안에 key 최소값 탐색과 인접노드의 key, parent 값 갱신으로 인하여 시간복잡도는 O(n²)와 같습니다.
O(n²)이 소요되는 주된 원인은 MST 트리에 추가할 key 값이 최소인 노드 탐색때문입니다. 다음 글에서는 프림 알고리즘의 시간복잡도를 개선하도록 하겠습니다.
5. 프림 알고리즘 O(m log n)
key의 최소값 탐색을 개선하기 위해서 우선순위 큐를 사용합니다.
public void primMST2(int start)
{
// MST 트리에 속한 노드와 자신을 연결하는 간선들 중
// 가중치가 최소인 간선 (u,v)의 가중치를 의미함.
int[] key = new int[V];
// 최소 가중치인 간선 (u,v)의 끝점 u를 의미함.
int[] parent = new int[V];
// 모든 노드의 key값과 parent값을 초기화
for(int u=0; u<V; u++)
{
key[u] = Integer.MAX_VALUE;
parent[u] = u;
}
PriorityQueue<Node<E>> nodes = new PriorityQueue<Node<E>>();
for(Node<E> node : map.values())
{
nodes.add(node);
}
// start 노드에서부터 시작함
// 시작 노드는 가중치가 없기 때문에 0으로 설정함
key[start] = 0;
int v = 0;
while(!nodes.isEmpty()) // MST 집합의 개수가 V개가 될때까지 반복함
{
int u = nodes.poll().num;
// u의 인접노드의 key값과 parent값 갱신
for(Node<E> node : adj.get(u))
{
v = node.num;
if(key[v] > edges[u][v] && nodes.contains(map.get(v)))
{
key[v] = edges[u][v];
parent[v] = u;
}
}
}
// MST 결과 출력
printMST(key, parent);
}
References
source code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph09_prim_mst
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][Graph] 최단 경로(Shortest Path) #2 최단 경로 문제, Dijkstra 알고리즘 (0) | 2022.02.22 |
|---|---|
| [알고리즘][Graph] 최단 경로(Shortest Path) #1 최단 경로 문제, Bellman-Ford 알고리즘 (0) | 2022.02.21 |
| [알고리즘][Graph] 최소 비용 신장 트리 #3 크루스칼(Kruskal) 알고리즘의 싸이클 검사와 구현 (0) | 2022.02.09 |
| [알고리즘][Graph] Disjoint Set #2 Union By Rank와 Path Compression (0) | 2022.02.08 |
| [알고리즘][Graph] Disjoint Set #1 무방향 그래프에서 싸이클 탐색 (0) | 2022.02.08 |