2022. 2. 9. 14:27ㆍAlgorithm
학습목표
1. 싸이클 검사의 수행과정을 학습
2. Java언어 기반 크루스칼 알고리즘 구현 학습
3. 크루스칼 알고리즘의 시간복잡도 계산을 학습
1. 싸이클 검사
크루스칼 알고리즘을 수행하게되면 에지(edge)들중 가중치(weight)가 최소인 에지들을 결과 배열에 넣게됩니다. 이때 에지들을 넣기전에 싸이클을 검사해야 합니다. 싸이클이란 그래프의 특정 노드에서 출발하여 방향(edge)을 따라 다시 출발한 노드로 올 수 있는 상황을 싸이클이 발생하였다고 합니다. 최소 신장 트리(Minimum Spanning Tree)에서는 싸이클이 존재해서는 안되기 때문에 에지들을 정하기 전에 싸이클 검사를 수행하여야 합니다.
싸이클이 존재하는지 탐색하는 방법에는 Union-Find 알고리즘을 사용하여 탐색할 수 있습니다.
https://yonghwankim-dev.tistory.com/235
[알고리즘][Graph] Disjoint Set #1 무방향 그래프에서 싸이클 탐색
학습목표 1. Disjoint Set 자료구조에 대해서 학습 2. Disjoint Set 자료구조를 이용하여 그래프에 싸이클이 있는지 검사 1. Disjoint-Set 자료구조란 무엇인가? Disjoint-Set 자료구조는 서로 중복되지 않는 부
yonghwankim-dev.tistory.com
싸이클 검사 수행과정/
- 에지(u,v) 선택
- u가 속한 부분집합의 대표 원소(루트 원소)와 v가 속한 부분집합의 대표 원소를 비교함 (find(u), find(v))
- 만약 같다면 싸이클이 발생한 것이므로 선택 제외
- 만약 다르다면 u의 부분집합과 v의 부분집합을 합집합함 (union(u,v))하고 결과배열(최소 신장 트리 배열)에 에지(u,v)를 추가함
- n-1개의 에지가 선택될때까지 1~2번 과정을 반복함.
다음은 무방향 그래프의 노드들을 각각의 부분집합(Disjoint-Set)으로 두고 크루스칼 알고리즘 수행 도중 사이클이 존재하는지 탐색하는 과정의 그림입니다.

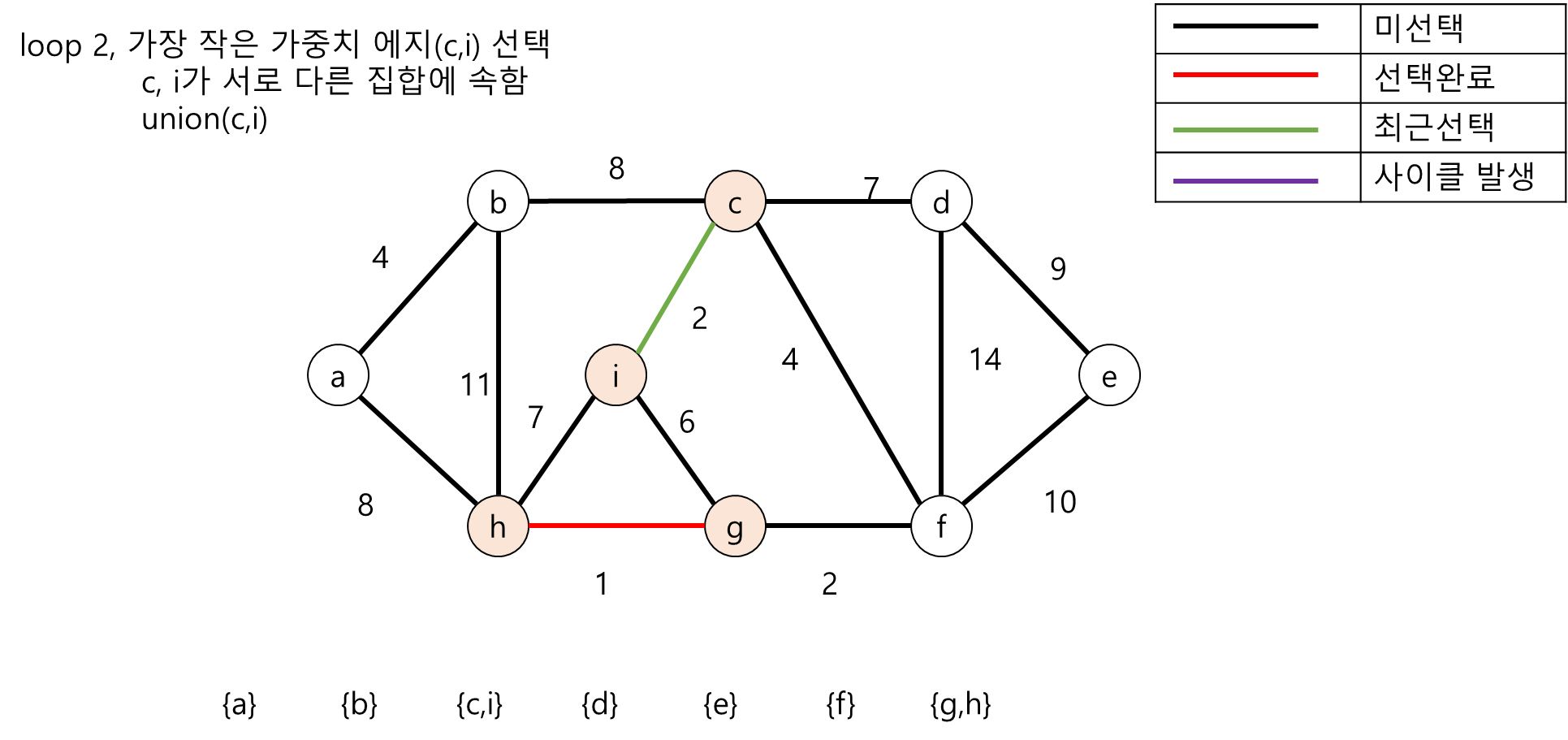

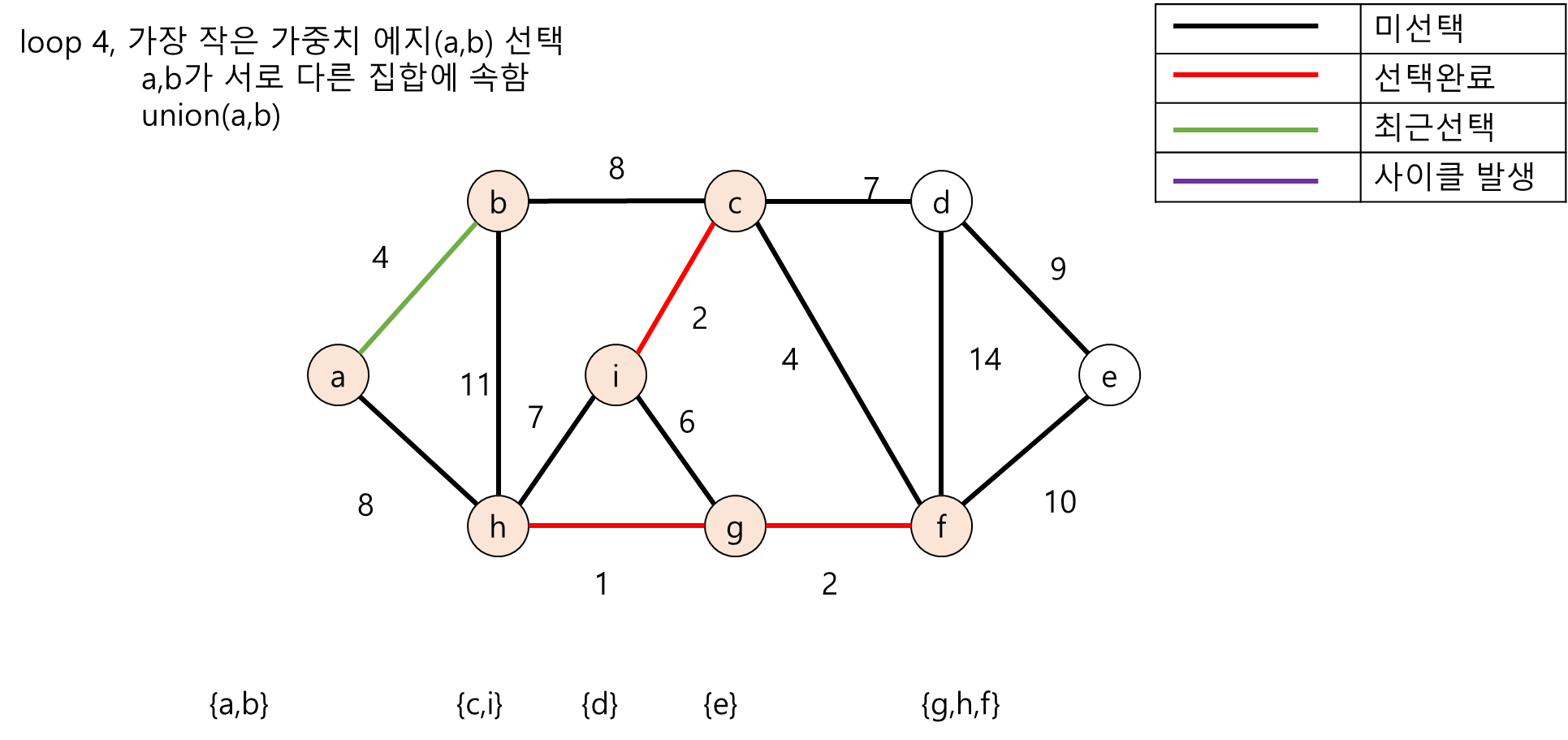

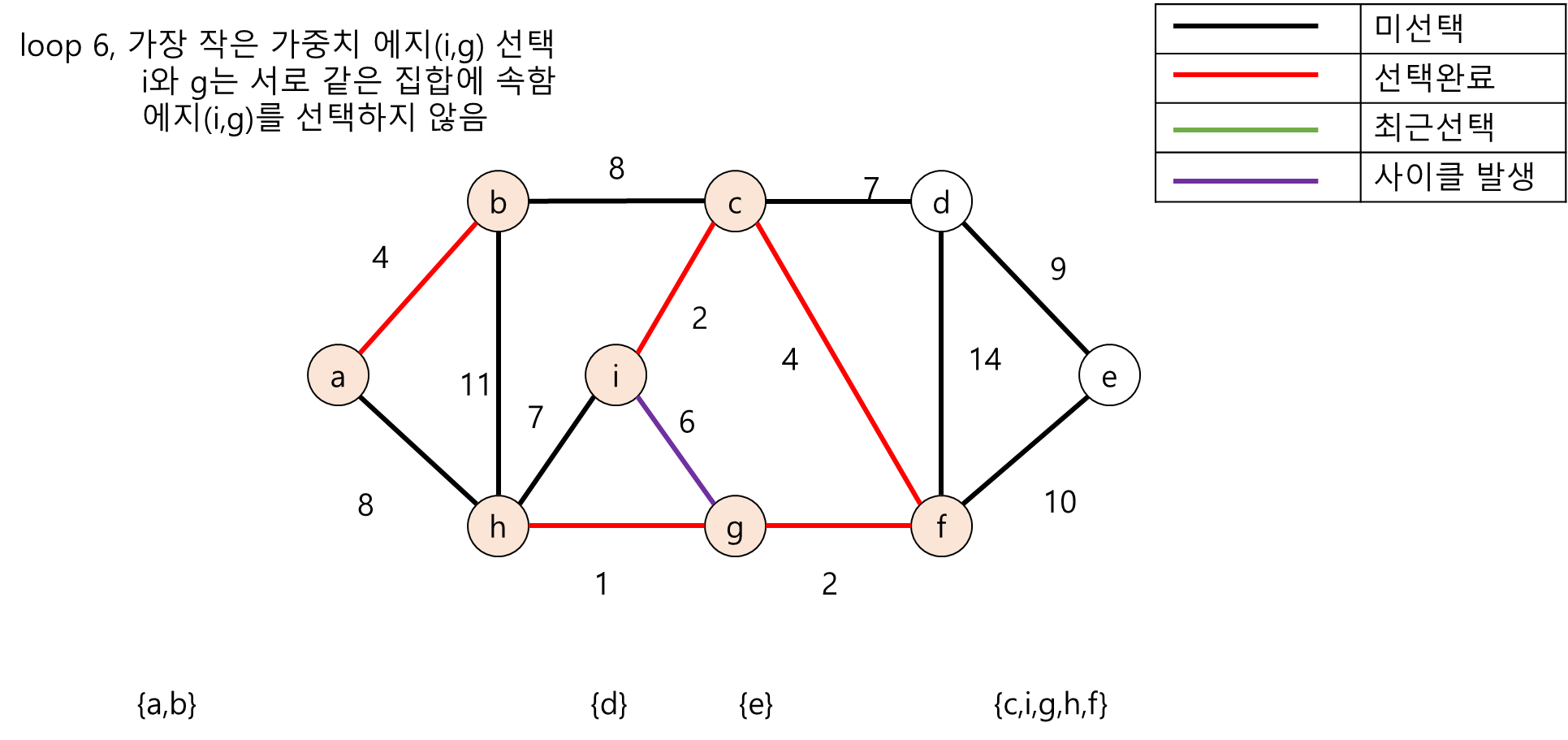
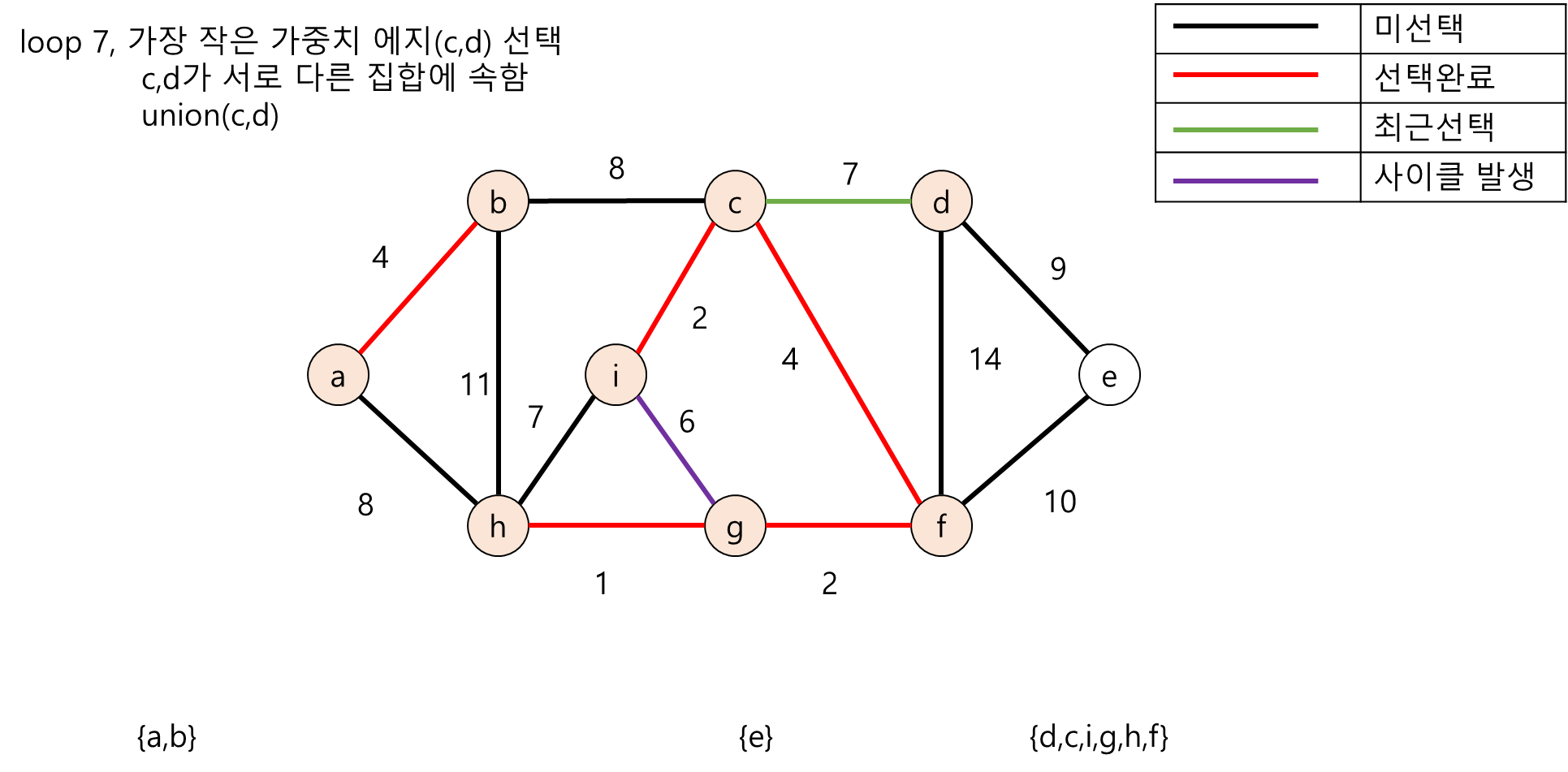
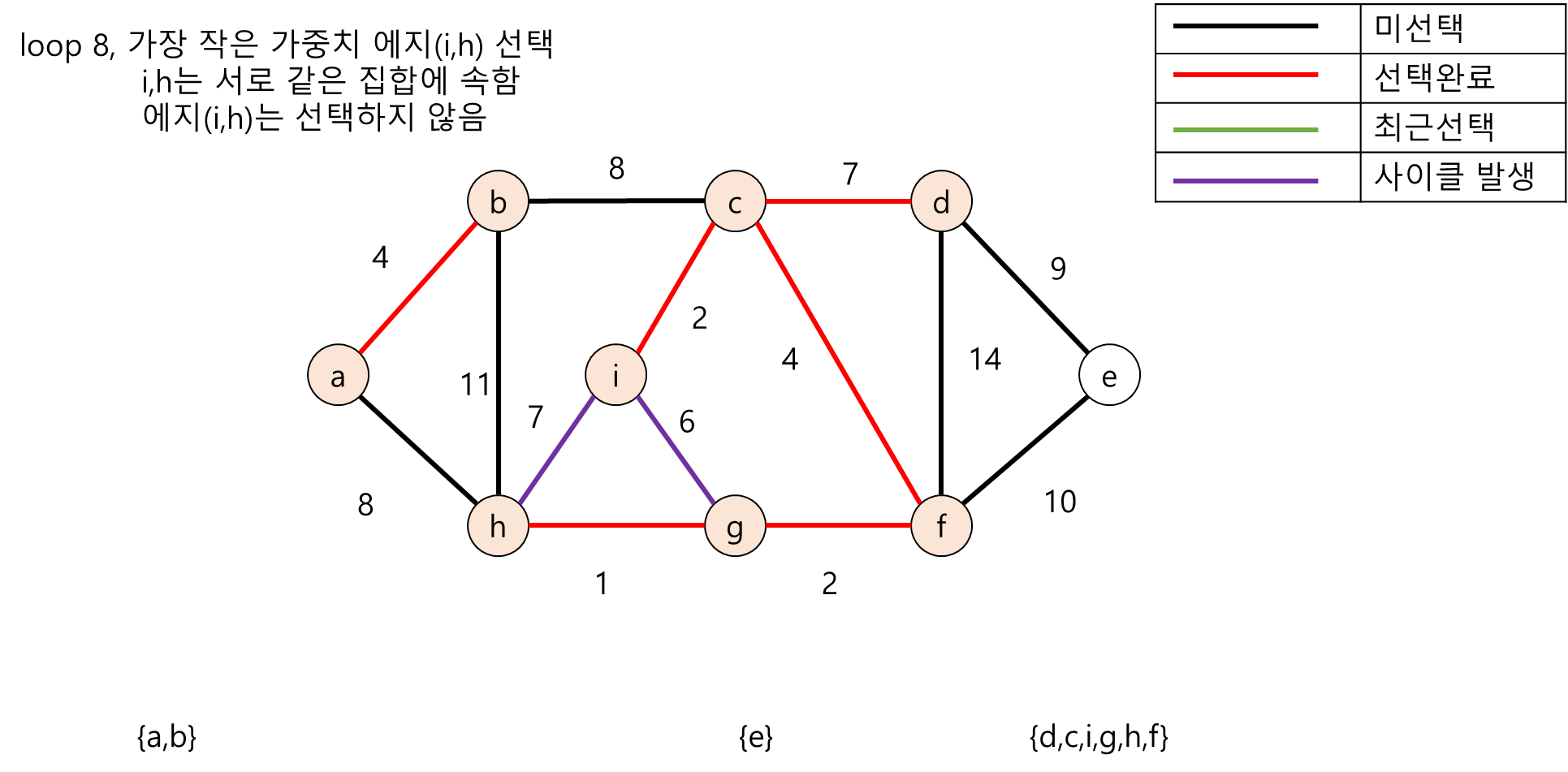
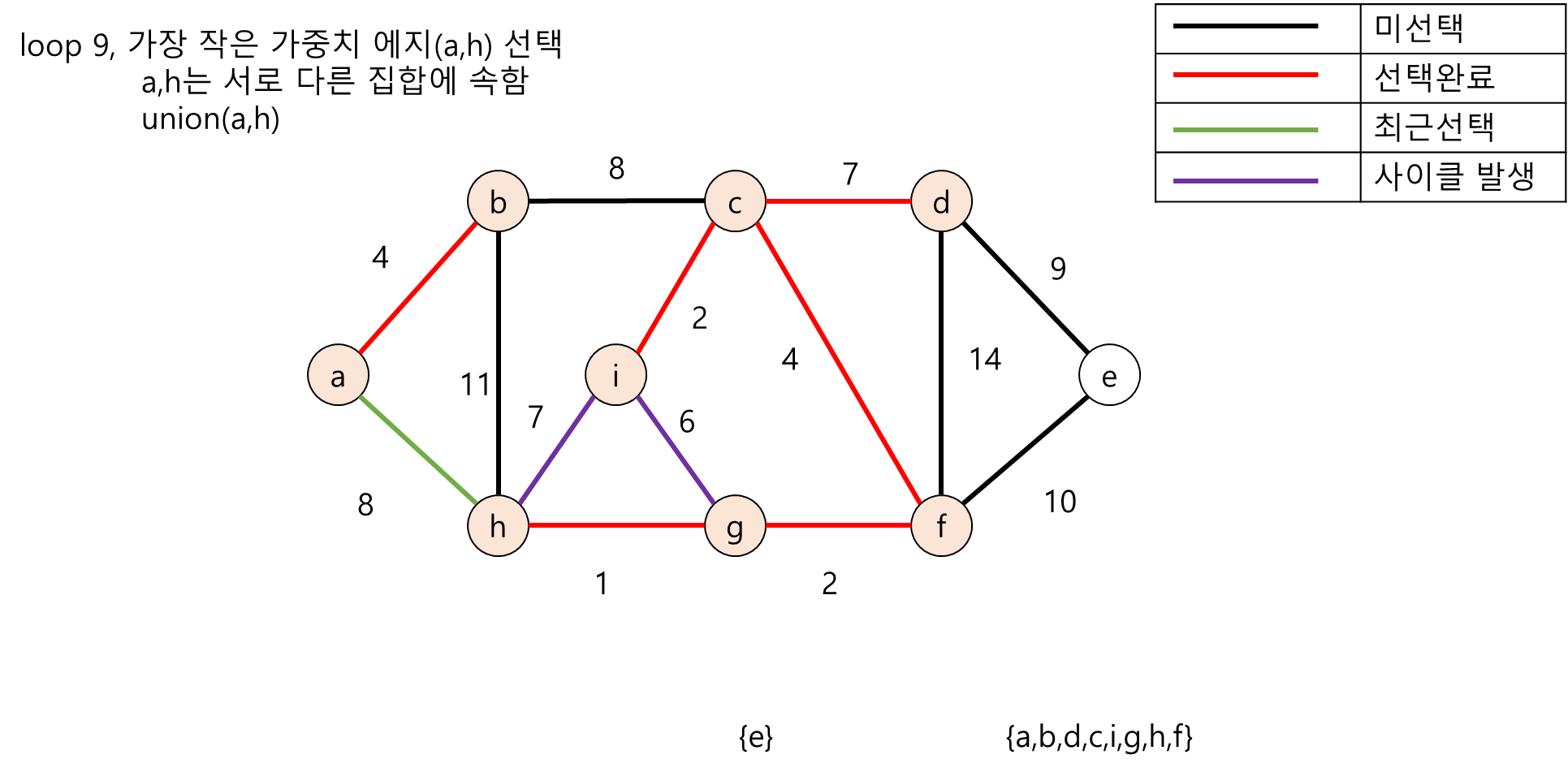
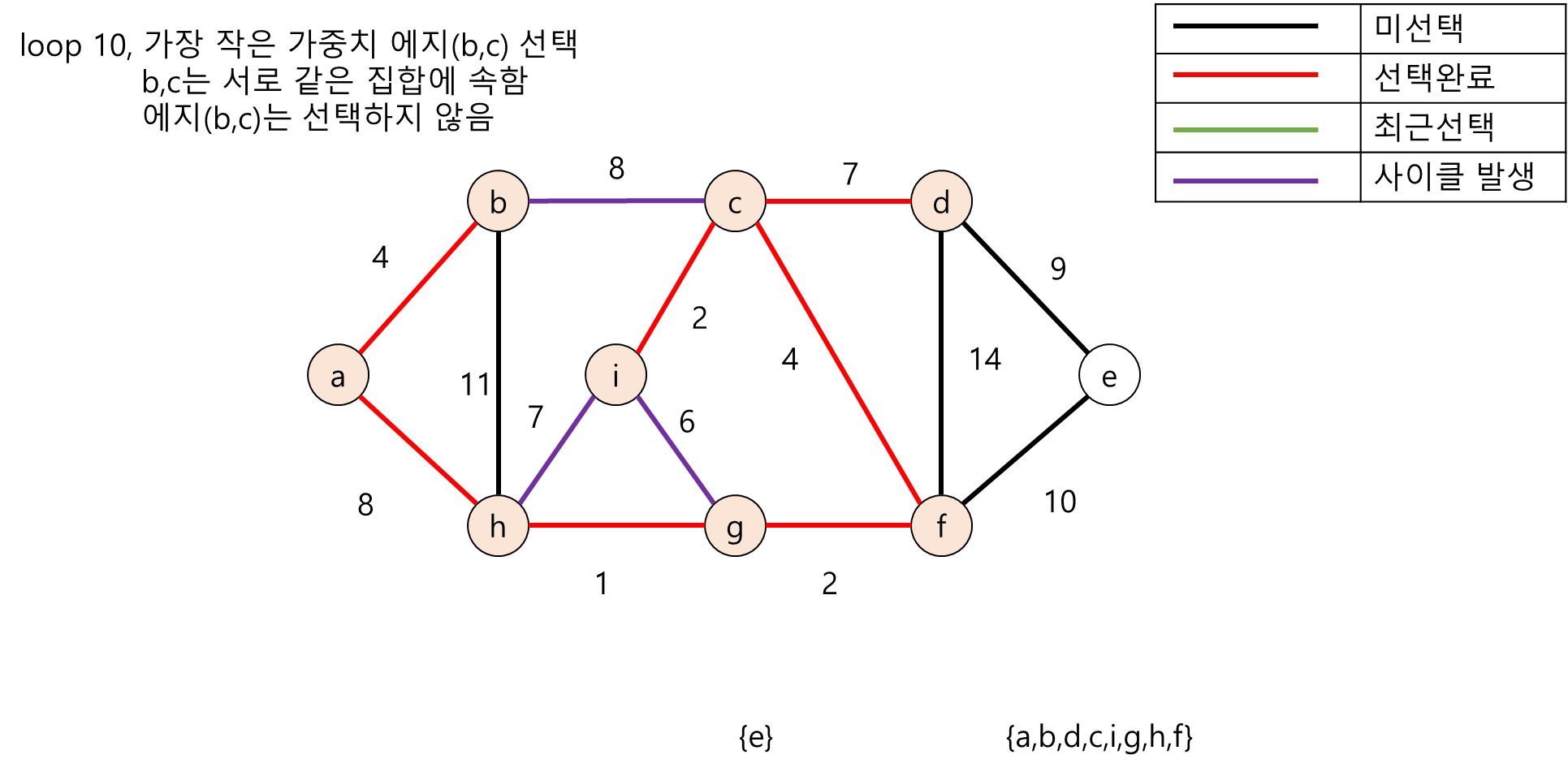
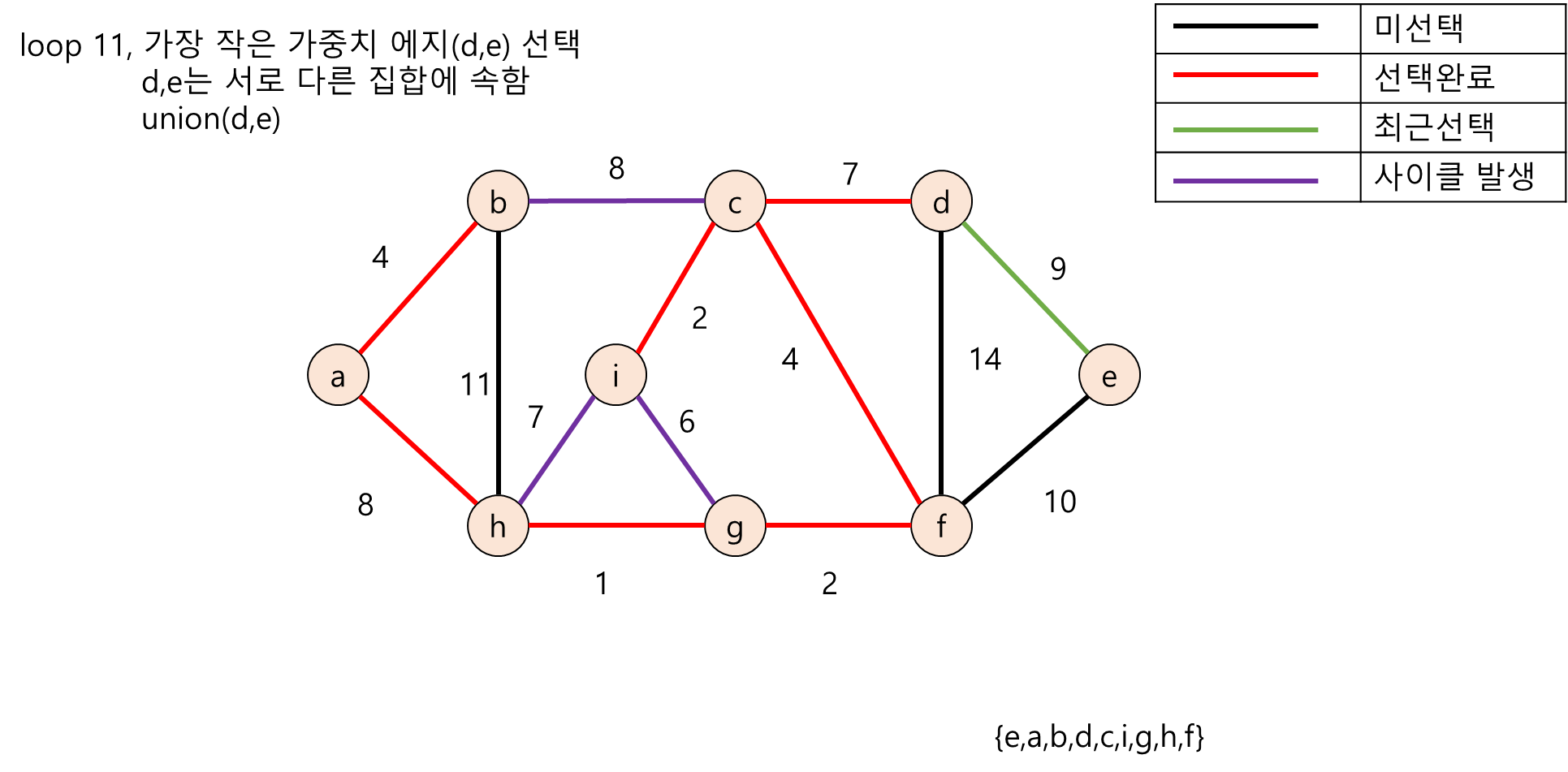
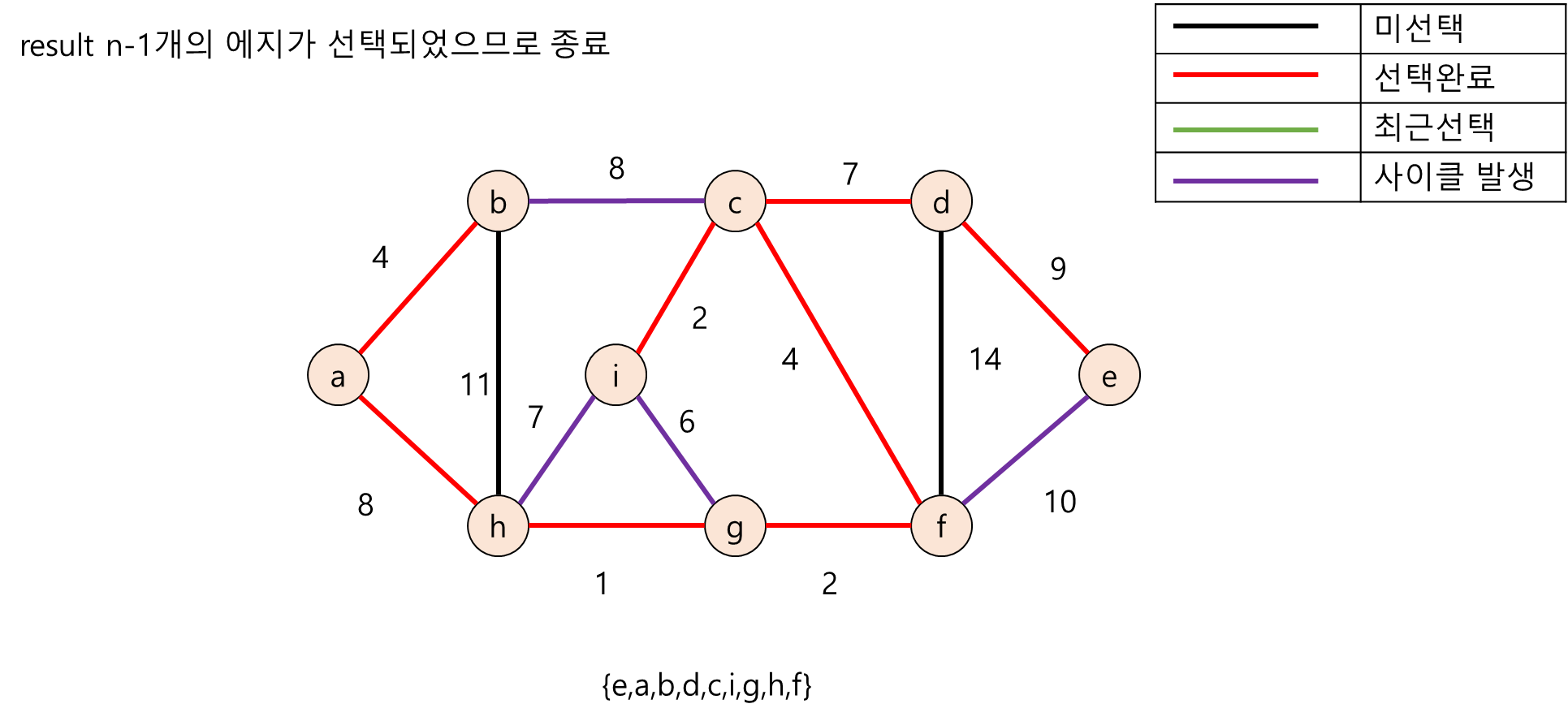
2. Java언어 기반 크루스칼 알고리즘 구현
public class UndirectedGraph implements Graph{
int V,E; // V : 정점의 개수, E : 간선의 개수
ArrayList<Edge> edge; // 간선들의 리스트
public UndirectedGraph(int v, int e) {
V = v;
E = e;
edge = new ArrayList<>();
}
// 간선 추가
public void addEdge(int src, int dest, int weight) {
edge.add(new Edge(src,dest, weight));
}
// 원소 i가 속해있는 부분집합의 대표 원소(트리의 루트 원소)를 탐색함
// 경로 압축(Path Compression) 기술 사용함
// 시간복잡도 : O(log*N)
public int find(Subset[] subsets, int i)
{
if(subsets[i].parent!=i)
{
subsets[i].parent = find(subsets, subsets[i].parent);
}
return subsets[i].parent;
}
// x가 속해있는 부분집합과 y가 속해있는 부분집합을 합집합함
// rank가 더작은 쪽이 rank 큰 트리쪽의 자식으로 들어감
// x.rank=y.rank인 경우 y 트리의 자식으로 들어가고 y.rank+1함
public void union(Subset[] subsets, int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if(subsets[xroot].rank < subsets[yroot].rank)
{
subsets[xroot].parent = yroot;
}
else if(subsets[xroot].rank > subsets[yroot].rank)
{
subsets[yroot].parent = xroot;
}
else
{
subsets[xroot].parent = yroot;
subsets[yroot].rank++;
}
}
// 무방향 그래프에서 최소 가중치 신장 트리를 탐색함
// 시간복잡도 : O(|E| log |E|)
public void kruskalMST()
{
Edge[] result = new Edge[V]; // 최소 가중치가 들어있는 간선 배열
Subset[] subsets = new Subset[V]; // 부분집합 배열
// O(|V|)
for(int i=0;i<V;i++)
{
result[i] = new Edge();
subsets[i] = new Subset(i,0);
}
// O(|E|log|E|)
edge.sort(new Comparator<Edge>() {
@Override
public int compare(Edge e1, Edge e2) {
return e1.weight - e2.weight;
}
});
int i=0;
int e=0;
// O(|E|)
// union-find 시간복잡도(union by rank and path compression 기술적용) : O(N+Mlog*N) = O(1)
while(e<V-1)
{
Edge next_edge = edge.get(i);
i++;
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
if(x!=y) // x!=y이면 싸이클이 발생하지 않음, x==y이면 싸이클 발생
{
result[e] = next_edge;
union(subsets, x,y);
e++;
}
}
System.out.println("Following are the edges in the constructed MST");
int minimumCost = 0;
int edge_n = result.length-1; // 간선의 개수는 정점의 개수-1개
for(i=0;i<edge_n;i++)
{
System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);
minimumCost += result[i].weight;
}
System.out.println("Minimum Cost Spanning Tree " + minimumCost);
}
}public class Driver {
public static void main(String[] args) {
int V = 4;
int E = 5;
UndirectedGraph graph = new UndirectedGraph(V, E);
graph.addEdge(0, 1, 10);
graph.addEdge(0, 2, 6);
graph.addEdge(0, 3, 5);
graph.addEdge(1, 3, 15);
graph.addEdge(2, 3, 4);
graph.kruskalMST();
}
}Following are the edges in the constructed MST
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Minimum Cost Spanning Tree 19
3. 크루스칼 알고리즘의 시간복잡도
V는 노드의 개수, E는 간선의 개수, M은 find 연산의 횟수, find 연산의 시간복잡도는 O(log₂*N)
- 부분집합(subsets) 생성 : O(|V|)
- 간선(Edge) 오름차순 정렬 : O(|E|log₂|E|)
- 최소 가중치 간선 선택 및 Union-Find 알고리즘 수행 : O(|E|) * (O(N+Mlog₂*N)=O(1)) = O(|E|)
- 크루스칼 알고리즘 시간복잡도 : O(|E|log₂|E|)
References
Source Code : https://github.com/yonghwankim-dev/inflearn_algorithm/tree/master/graph/graph08_kruskal_mst
Geeks For Geeks : https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/
[인프런] 영리한 프로그래밍을 위한 알고리즘 강좌
'Algorithm' 카테고리의 다른 글
| [알고리즘][Graph] 최단 경로(Shortest Path) #1 최단 경로 문제, Bellman-Ford 알고리즘 (0) | 2022.02.21 |
|---|---|
| [알고리즘][Graph] 최소 비용 신장 트리 #4 프림(Prim's) 알고리즘의 개념과 수행과정 (0) | 2022.02.15 |
| [알고리즘][Graph] Disjoint Set #2 Union By Rank와 Path Compression (0) | 2022.02.08 |
| [알고리즘][Graph] Disjoint Set #1 무방향 그래프에서 싸이클 탐색 (0) | 2022.02.08 |
| [알고리즘][Graph] 싸이클(Cycle) #2 무방향 그래프에서 싸이클이 있는지 탐색 (0) | 2022.02.07 |