정렬, 기수 정렬(Radix Sort)
2022. 1. 20. 17:12ㆍDataStructure
학습목표
1. 기수 정렬이 무엇인지 학습
2. 기수 정렬의 수행과정을 학습
3. 기수 정렬을 구현
4. 기수 정렬의 시간복잡도에 대해서 학습
1. 기수 정렬(Radix Sort)란 무엇인가?
기수 정렬은 우편번호, 자리수 등의 기준을 만들어 기준에 따라 숫자를 분류하여 정렬하는 방법입니다.
예를 들어, 4자리 숫자를 일의 자리의 숫자, 십의 자리의 숫자, 백의 자리의 숫자, 천의 자리의 숫자에 따라 분류하여 정렬할 수 있습니다.
2. 기수 정렬의 수행 과정
기수 정렬의 수행 과정은 다음과 같습니다.
- 0~9까지의 Bucket(Queue 구조) 리스트를 준비합니다.
- 모든 데이터에 대하여 가장 낮은 자리수에 해당하는 Bucket에 차례대로 데이터를 추가합니다.
- 0부터 차례대로 버킷에서 데이터를 가져옵니다. (제거)
- 가장 높은 자리수를 기준으로 하여 자리수를 높여가며 2~3번 과정을 반복합니다.
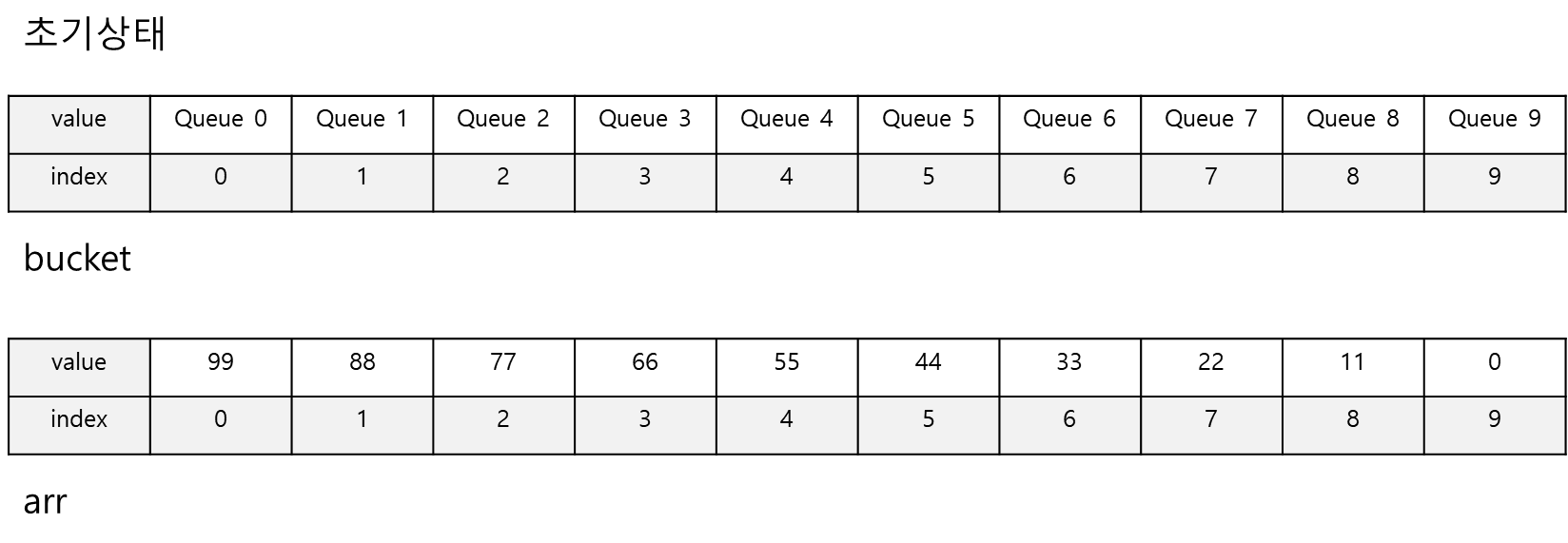
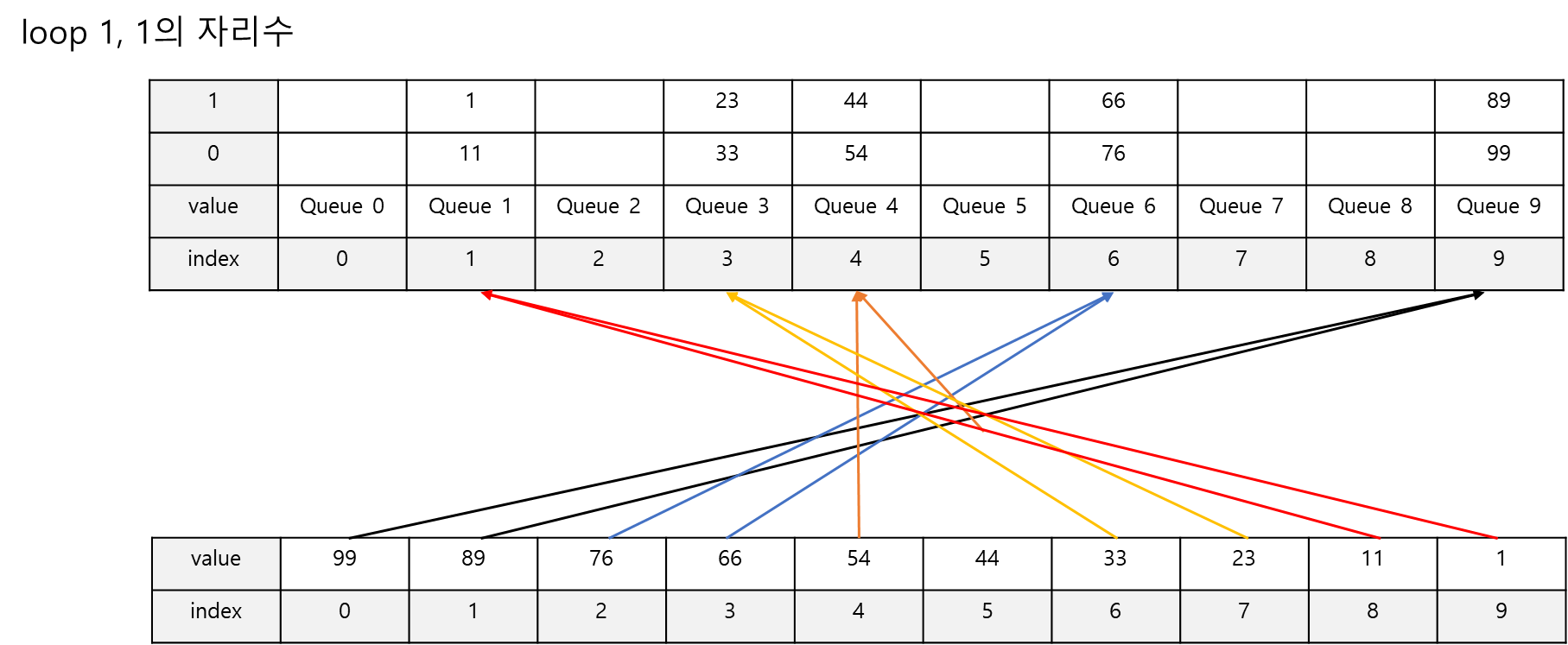
1의 자리 숫자부터 시작하여 각 1의 자리에 해당하는 Queue에 추가됩니다. 예를 들어 99같은 경우 일의 자리가 9이므로 9번째 인덱스의 큐에 삽입됩니다.
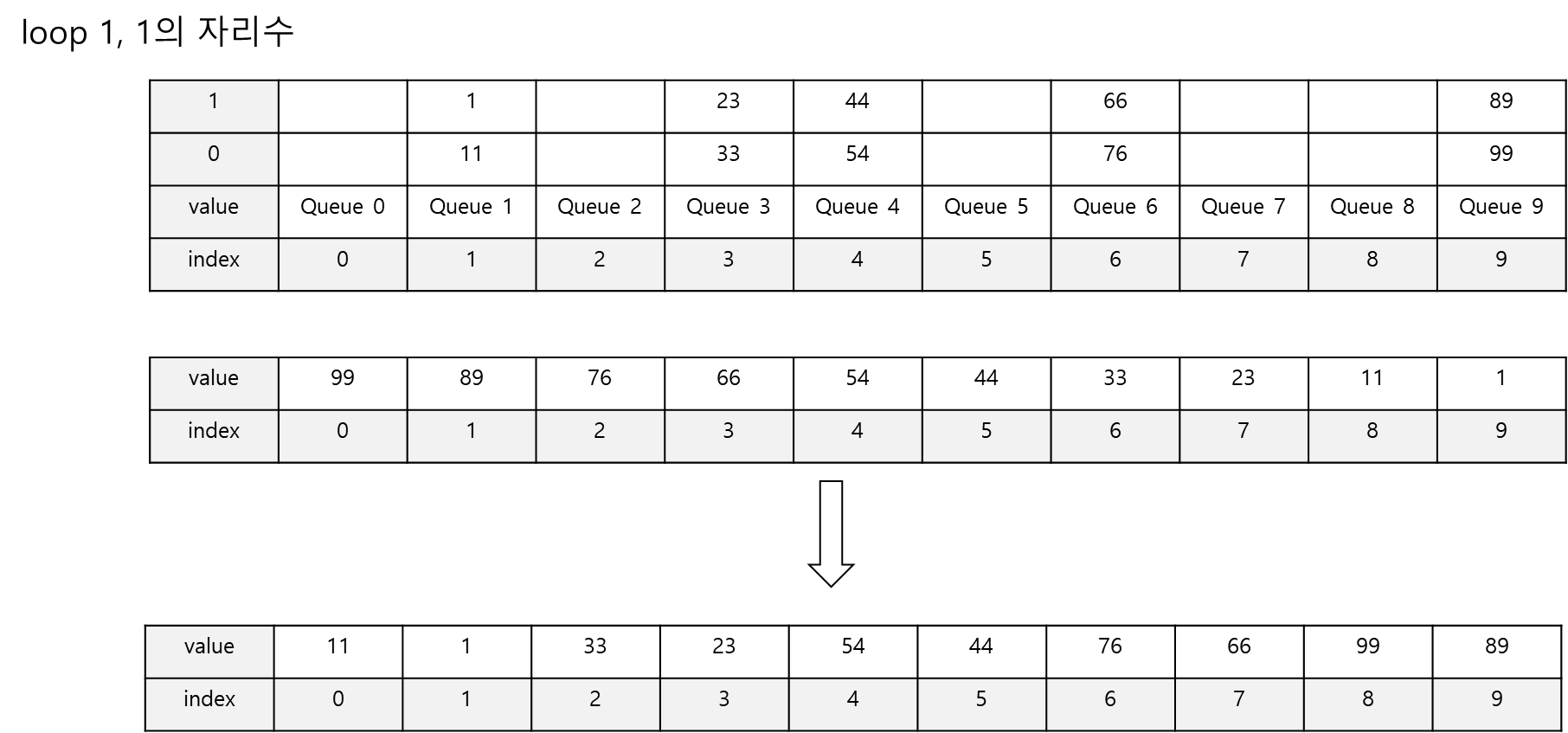
큐에 삽입을 마치면 다시 제일 앞쪽의 큐(0~9)부터 큐에서 데이터를 제거하면서 배열의 앞쪽에서부터 데이터를 채워나갑니다. 큐의 데이터를 제거한 결과 배열은 {11,1,33,23,54,44,76,66,99,89}로 채워집니다.

이번에는 10의 자리의 숫자에 따라서 다시 큐에 추가됩니다. 예를 들어 11같은 경우 11의 10자리 숫자는 1이므로 1번째 큐에 추가됩니다.
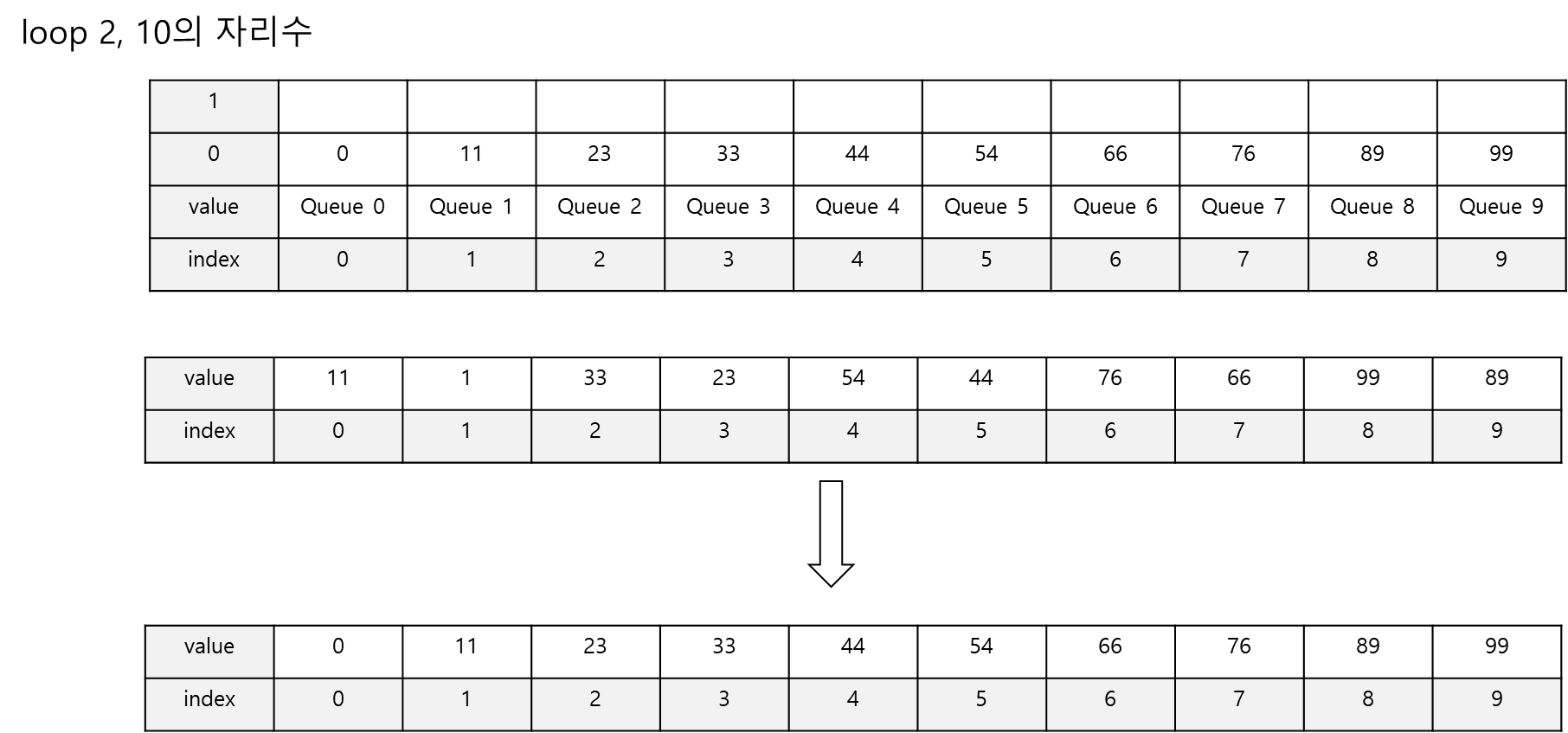
ㅈ추가된 큐를 앞쪽에서부터 제거하여 배열은 {0,11,23,33,44,54,66,76,89,99}로 채워집니다. 최대 자리수가 10의 자리임으로 정렬을 종료합니다.

3. 기수 정렬의 구현
public class RadixSort {
private static int getMaxLength(int[] arr)
{
int maxSize = 0;
for(int i=0;i<arr.length;i++)
{
int length = (int)Math.log10((double)arr[i])+1;
if(maxSize<length)
{
maxSize = length;
}
}
return maxSize;
}
public static void sort(int[] arr)
{
List<Queue<Integer>> bucket = new LinkedList<Queue<Integer>>();
int n = arr.length;
int maxSize = getMaxLength(arr);
int powed=1; // 자리수, 1,10,100,... 10^n
int index=0;
// 버킷 생성
for(int i=0;i<10;i++)
{
bucket.add(new LinkedList<Integer>());
}
// 자리수가 가장 큰 만큼 전체 반복문을 반복함
for(int i=1;i<=maxSize;i++)
{
for(int j=0;j<n;j++)
{
// 각 자리수의 맞는 index의 bucket에 넣음
bucket.get((arr[j]/powed)%10).add(arr[j]);
}
// 버킷에서 데이터를 가지고 옴
for(int k=0;k<10;k++)
{
int bucket_num = bucket.get(k).size();
for(int s=0;s<bucket_num;s++)
{
arr[index] = bucket.get(k).poll();
index++;
}
}
index = 0;
powed *= 10;
}
}
public static void main(String args[])
{
int[] arr = {99,88,77,66,55,44,33,22,11,0};
System.out.println(Arrays.toString(arr));
sort(arr);
System.out.println(Arrays.toString(arr));
}
}[99, 88, 77, 66, 55, 44, 33, 22, 11, 0]
[0, 11, 22, 33, 44, 55, 66, 77, 88, 99]
4. 기수 정렬의 시간복잡도
- O(dn) : d는 최대 자리수, 예를 들어 {11,22,111}이라는 배열이 존재하면 최대 자리수는 3을 의미합니다. n은 정렬할 데이터 개수입니다. 따라서 최대 1개의 데이터당 최대 자리수만큼 옮겨 질 수 있다는 의미입니다.
시간복잡도가 O(dn)에서 d는 상수이므로 O(n)와 같이 표현하여 빠른 정렬방법이지만 실제로는 숫자를 복사하는 과정이 너무 많기 때문에 수행 속도가 느립니다. 그래서 컴퓨터에서는 사용하기 어렵고 일상 생활에서 우편물을 정려할 때와 같이 기계적으로 정렬할 때 많이 쓰입니다.
References
source code : https://github.com/yonghwankim-dev/DataStruct/tree/main/sort/radix_sort/implement
[부스트코스] 자바로 구현하고 배우는 자료구조
06 정렬 알고리즘 - 기수 정렬(Radix Sort)
'DataStructure' 카테고리의 다른 글
| 선형데이터구조, 연결리스트(LinkedList) #9 원형 연결리스트(Circular LinkedList) (0) | 2022.05.04 |
|---|---|
| 정렬, 정렬 시간복잡도 (0) | 2022.01.20 |
| 정렬, 퀵 정렬(Quick Sort) (0) | 2022.01.18 |
| 정렬, 합병 정렬(Merge Sort) (0) | 2022.01.10 |
| 정렬, 쉘 정렬(Shell Sort) (0) | 2022.01.10 |