2022. 1. 10. 15:05ㆍDataStructure
1. 합병 정렬(Merge Sort)
퀵 정렬과 같이, 합병 정렬은 분할 정복 알고리즘(Divide and Conquer)입니다. 합병 정렬은 리스트의 요소가 한개가 될때까지 리스트를 절반으로 나누는 과정을 수행합니다. 그리고 리스트의 요소가 각각 1개로 나누어지면 다시 정렬하면서 병합하는 과정을 수행합니다. 아래의 merge() 메서드는 절반으로 나누어진 두 리스트를 병합하는데 사용됩니다. 이것을 수두코드로 표현하면 아래와 같습니다.
mergeSort(arr[], left, right)
if right > 1
1. 리스트를 절반으로 나누기 위해서 중간점을 탐색합니다.
middle = (left + right) / 2
2. 첫번째 절반의 리스트에 대해서 합병정렬을 재귀적인 호출합니다.
mergeSort(arr, left, middle)
3. 두번째 절반의 리스트에 대해서 합병정렬을 재귀적인 호출합니다.
mergeSort(arr, middle+1, right)
4. 정렬된 두 리스트를 병합합니다.
merge(arr, left, middle, right)
다음 그림은 리스트 {38,27,43,3,9,82,10}에 대한 합병 정렬의 예시입니다.
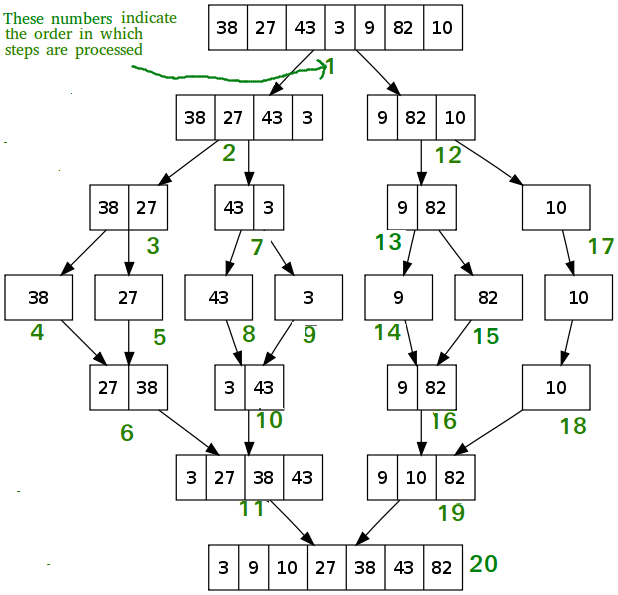
위의 그림을 보면 하나였던 리스트가 재귀적으로 절반씩 나누어져 각각의 리스트의 크기가 1개가 될때까지 수행됩니다. 그리고 다시 정렬하면서 병합하여 병합정렬을 완성시킵니다.
아래의 그림은 두 리스트 {3,27,38,43}과 {9,10,82}의 병합과정을 나타낸 그림입니다.
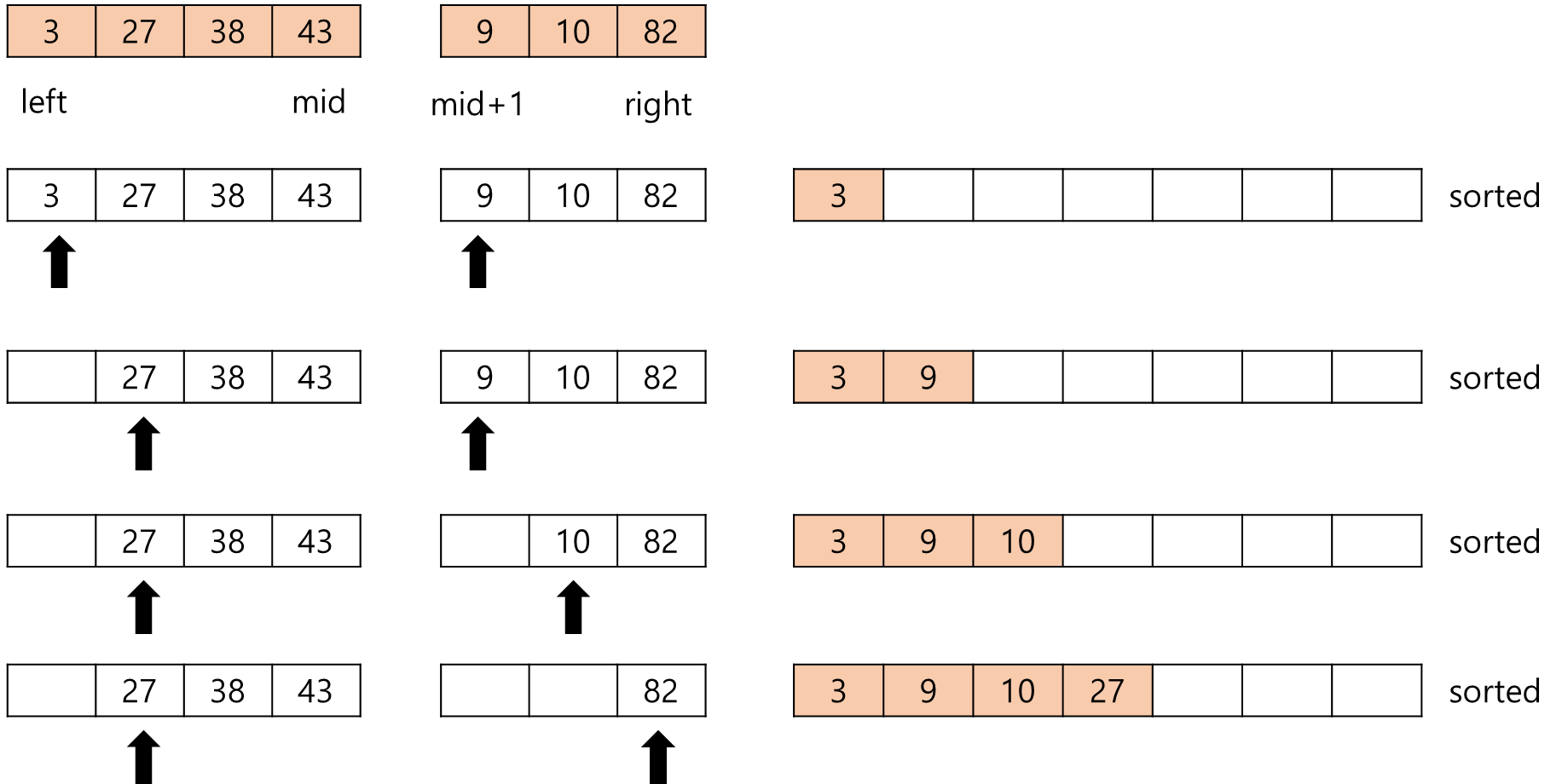
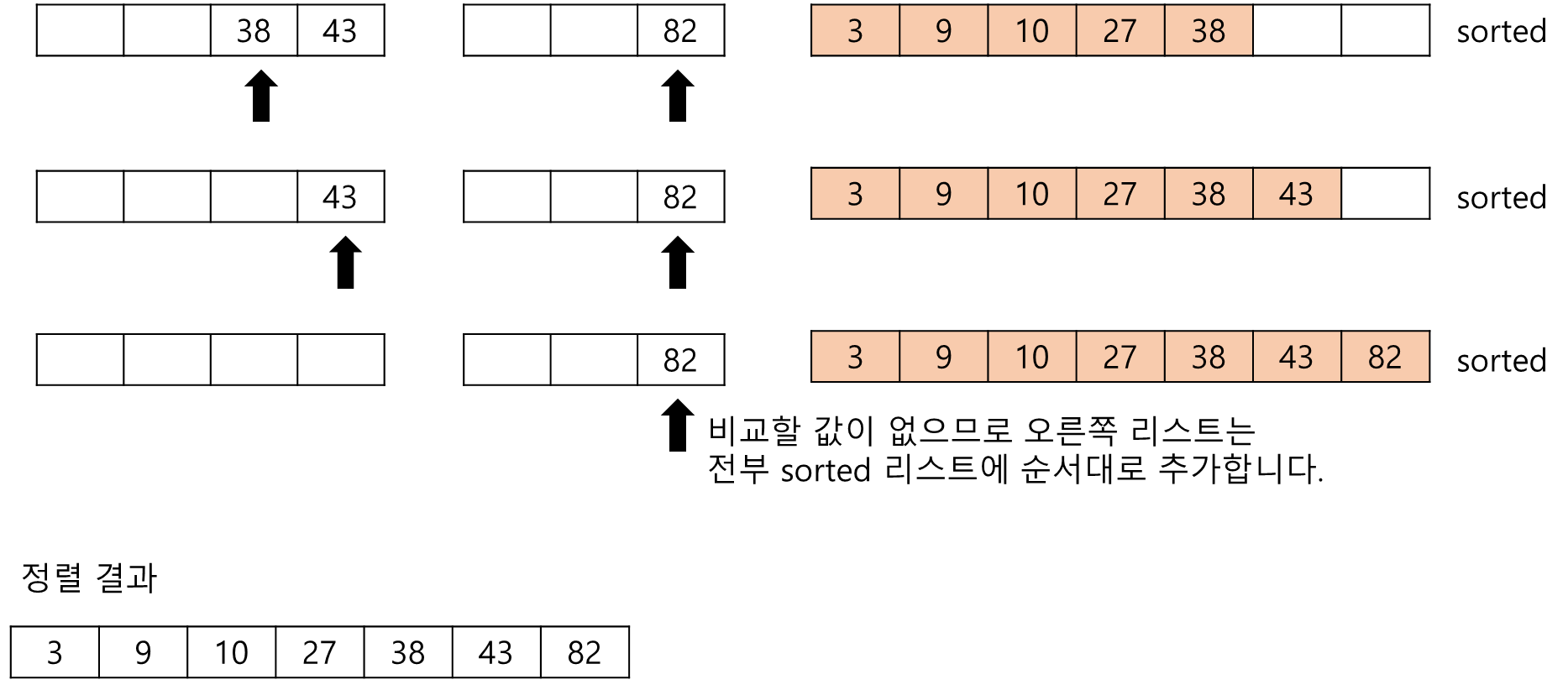
2. 합병 정렬 소스코드 구현
public class MergeSort {
public static void merge(int[] arr, int left, int middle, int right)
{
int n1 = middle-left+1;
int n2= right-middle;
int[] left_arr = new int[n1];
int[] right_arr = new int[n2];
for(int i=0; i<n1;i++)
{
left_arr[i] = arr[left+i];
}
for(int j=0; j<n2; j++)
{
right_arr[j] = arr[middle+1+j];
}
int i=0, j=0;
int k=left;
// 대소를 비교하여 arr에 정렬된 요소를 저장합니다.
while(i<n1 && j<n2)
{
if(left_arr[i]<=right_arr[j])
{
arr[k] = left_arr[i];
i++;
}
else
{
arr[k] = right_arr[j];
j++;
}
k++;
}
// 왼쪽 배열의 남은 요소들을 저장합니다.
while(i<n1)
{
arr[k] = left_arr[i];
i++;
k++;
}
// 오른쪽 배열의 남은 요소를 저장합니다.
while(j<n2)
{
arr[k] = right_arr[j];
j++;
k++;
}
}
public static void sort(int[] arr, int left, int right)
{
if(left<right)
{
int middle = (left + right)/2;
sort(arr, left, middle);
sort(arr, middle+1, right);
merge(arr, left, middle, right);
}
}
}class MergeSortTest {
@Test
void test() {
int[] arr = {32,27,43,3,9,82,10};
System.out.println(Arrays.toString(arr));
MergeSort.sort(arr, 0, arr.length-1);
System.out.println(Arrays.toString(arr));
}
}[32, 27, 43, 3, 9, 82, 10]
[3, 9, 10, 27, 32, 43, 82]3. 병합 정렬의 시간복잡도
순환 호출의 깊이(합병 단계의 수)
레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2³의 경우 2³->2²->2¹->2⁰ 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있습니다. 이것을 일반화하면 n=2^k의 경우, k=log₂n 임을 알 수 있습니다.
각 합병 단계의 비교 연산
크기 1인 부분 배열 2개를 합병하는 데는 최대 2번의 비교 연산이 필요합니다. 부분 배열의 쌍이 4개이므로 8번의 비교연산이 필요합니다. 다음 단계에서는 크기 2인 부분 배열 2개를 합병하는 데 최대 4번의 비교연산이 필요합니다. 부분 배열의 쌍이 2개이므로 8번의 비교연산이 필요합니다. 마지막 단게에서는 크기 4인 부분 배열 2개를 합병하는데는 최대 8번의 비교 연산이 필요합니다. 부분 배열의 쌍이 1개이므로 1*8=8번의 비교 연산이 필요합니다. 이것을 일반화하면 하나의 합병 단계에서는 최대 n번의 비교 연산을 수행함을 알 수 있습니다.
각 합병 단계의 이동 연산
임시 배열에 복사했다가 다시 가져와야 되므로 이동 연산은 총 부분 배열에 들어 있는 요소의 개수가 n인 경우 레코드의 이동이 2n번 발생합니다.
위의 연산을 정리하여 합병 정렬의 시간복잡도를 구하면 다음과 같습니다.
T(n) = 비교횟수 + 이동횟수
비교횟수 = 순환호출의 깊이만큼의 합병단계 * 각 합병 단계의 비교 연산
= log₂n * n
= nlog₂n
이동횟수 = 순환호출의 깊이만큼의 합병단계 * 각 합병 단계의 이동연산
= log₂n * 2n
T(n) = nlog₂n + 2nlog₂n = 3nlog₂n = O(nlog₂n)
References
source code : https://github.com/yonghwankim-dev/DataStruct/tree/main/sort/merge_sort/implement
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
[부스트코스] 자바로 구현하고 배우는 자료구조, 합병정렬
[GeeksForGeeks] Merge Sort
'DataStructure' 카테고리의 다른 글
| 정렬, 기수 정렬(Radix Sort) (0) | 2022.01.20 |
|---|---|
| 정렬, 퀵 정렬(Quick Sort) (0) | 2022.01.18 |
| 정렬, 쉘 정렬(Shell Sort) (0) | 2022.01.10 |
| 정렬, 삽입정렬(Insertion Sort) (0) | 2022.01.07 |
| 정렬, 선택정렬(Selection Sort) (0) | 2022.01.06 |