비선형 데이터구조, 트리(Tree) #7 이진 탐색 트리 탐색(search) 및 추가(add)
2021. 9. 24. 13:22ㆍDataStructure
1. 이진 탐색 트리의 특징
- 특정 노드를 기준으로 왼쪽 서브트리는 특정 노드의 키값보다 작다
- 특정 노드를 기준으로 오른쪽 서브트리는 특정 노드의 키값보다 크다
- 왼쪽, 오른쪽 서브트리들의 노드들은 또다른 자식 서브트리로 구성된다.
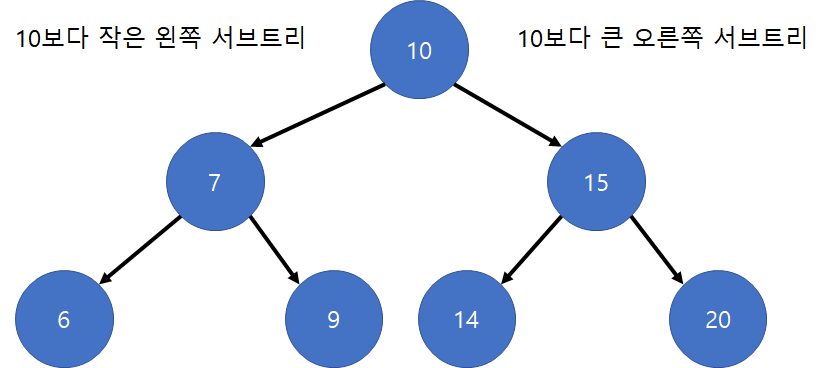
위의 이진 탐색 트리의 특징들은 탐색, 최솟값, 최대값과 같은 기능들을 빠르게 할 수 있도록 키 값들간에 순서를 제공합니다. 만약 트리에 순서가 없다면 모든 키값과 주어진 키값을 비교해야 합니다.
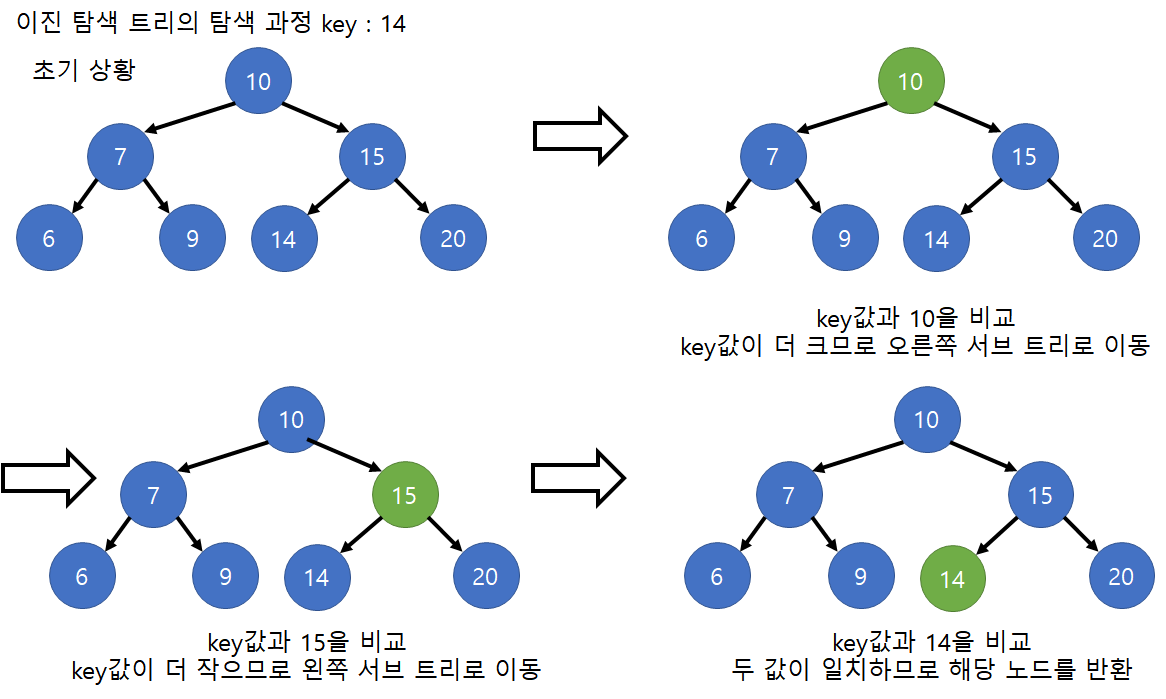
2. 이진 탐색 트리의 탐색 수행 과정
- 시작은 root 노드에서 시작합니다.
- 현재 노드와 탐색하고자 하는 key값을 비교합니다.
- key값이 현재 노드의 값보다 작으면 왼쪽 서브트리로 이동
- key값이 현재 노드의 값보다 크면 오른쪽 서브트리로 이동
- key값이 현재 노드의 값과 동일하면 해당 노드를 반환하고 종료
3. 이진 탐색 트리의 탐색 구현
// E 값을 가진 객체를 탐색
public Node<E> search(E data)
{
return search(root, data);
}
// root 노드를 기준으로 data 값을 가진 객체 탐색
private Node<E> search(Node<E> root, E data)
{
if(root==null)
{
return null;
}
if(((Comparable<E>)data).compareTo(root.data)<0)
{
return search(root.left, data);
}
else if(((Comparable<E>)data).compareTo(root.data)>0)
{
return search(root.right, data);
}
else
{
return root;
}
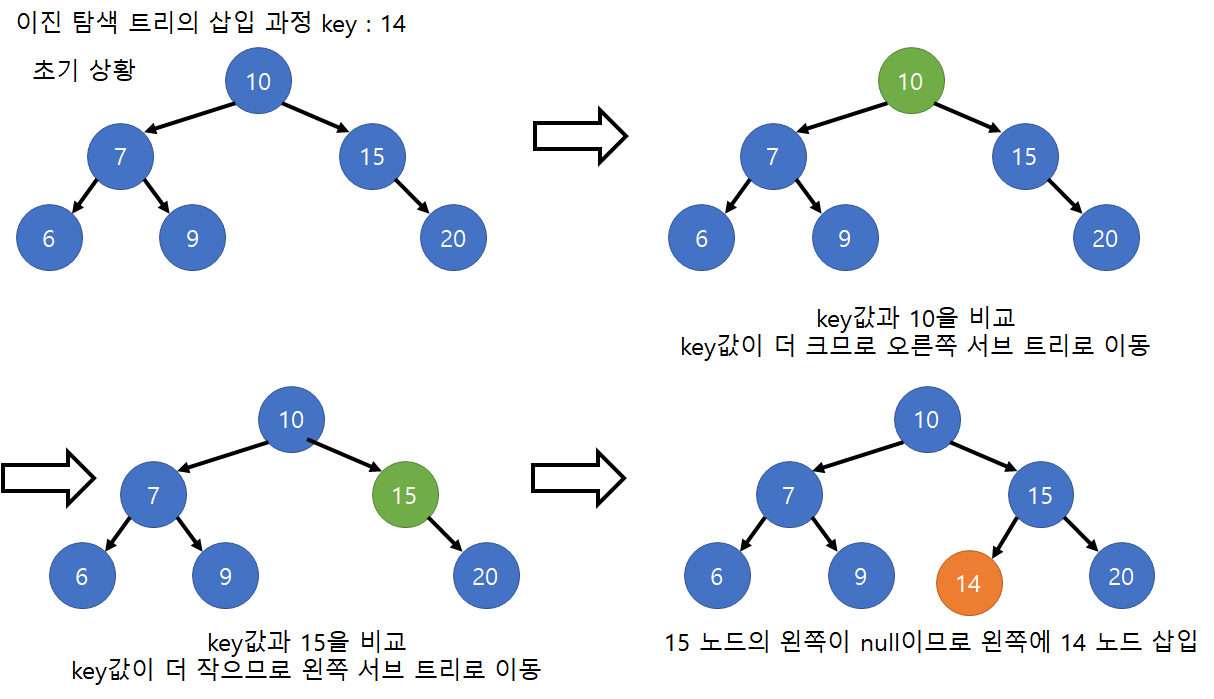
}3. 이진 탐색 트리의 추가 수행 과정
- 삽입시 Root 노드부터 시작합니다.
- Root노드와 삽입할 key값을 비교하여 key값이 Root노드보다 작으면 왼쪽 서브트리로 이동, key값이 Root노드보다 크면 오른쪽 서브트리로 이동, 재귀적인 연산이후 Root노드가 null이 될때까지 이동한다.
- 비어있는 Root노드에 노드 삽입
4. 이진 탐색 트리의 추가 구현
// obj 객체를 이진 탐색 트리에 추가
public void add(E obj){
if(root==null)
{
root = new Node<E>(obj);
}
else
{
add(root, obj);
}
currentSize++;
}
private void add(Node<E> root, E obj)
{
if(((Comparable<E>)obj).compareTo(root.data)>0) // go to the right
{
if(root.right==null)
{
root.right = new Node<E>(obj);
}
else
{
add(root.right, obj);
}
}
else if(((Comparable<E>)obj).compareTo(root.data)<0) // go to the left
{
if(root.left==null)
{
root.left = new Node<E>(obj);
}else
{
add(root.left, obj);
}
}
return;
} @Test
void addTest() {
BinarySearchTree<Integer> bst = new BinarySearchTree<Integer>();
bst.add(10);
bst.add(8);
bst.add(20);
bst.add(17);
bst.add(9);
bst.inorderTraversal(); // Expected Output : 8 9 10 17 20
}Output
8 9 10 17 20
References
source code : https://github.com/yonghwankim-dev/DataStruct/tree/main/Tree/BST/Implement
https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
[부스트코스] 자바로 구현하고 배우는 자료구조
'DataStructure' 카테고리의 다른 글
| 비선형 데이터구조, 트리(Tree) #9 TreeSet in Java (0) | 2021.09.28 |
|---|---|
| 비선형 데이터구조, 트리(Tree) #8 이진 탐색 트리 삭제(Delete) (0) | 2021.09.27 |
| 비선형 데이터구조, 트리(Tree) #6 이진 트리의 삭제(Delete) (0) | 2021.09.24 |
| 비선형 데이터구조, 트리(Tree) #5 이진 트리의 삽입(Insert) (0) | 2021.09.24 |
| 비선형 데이터구조, 트리(Tree) #3 이진 트리의 종류 (0) | 2021.09.23 |