비선형 데이터구조, 트리(Tree) #6 이진 트리의 삭제(Delete)
2021. 9. 24. 11:12ㆍDataStructure
1. 개요
이진 트리에서 삭제 기능을 구현합니다. 삭제 기능의 전체적인 과정은 삭제될 노드를 탐색하고 삭제하고 남은 빈 자리를 이진 트리에서 제일 오른쪽에 위치하는 노드로 대체합니다. 그리고 노드가 2개로 중복되었으므로 제일 오른쪽에 존재하는 노드를 삭제하면서 종료합니다.
2. 이진트리 삭제 수행과정
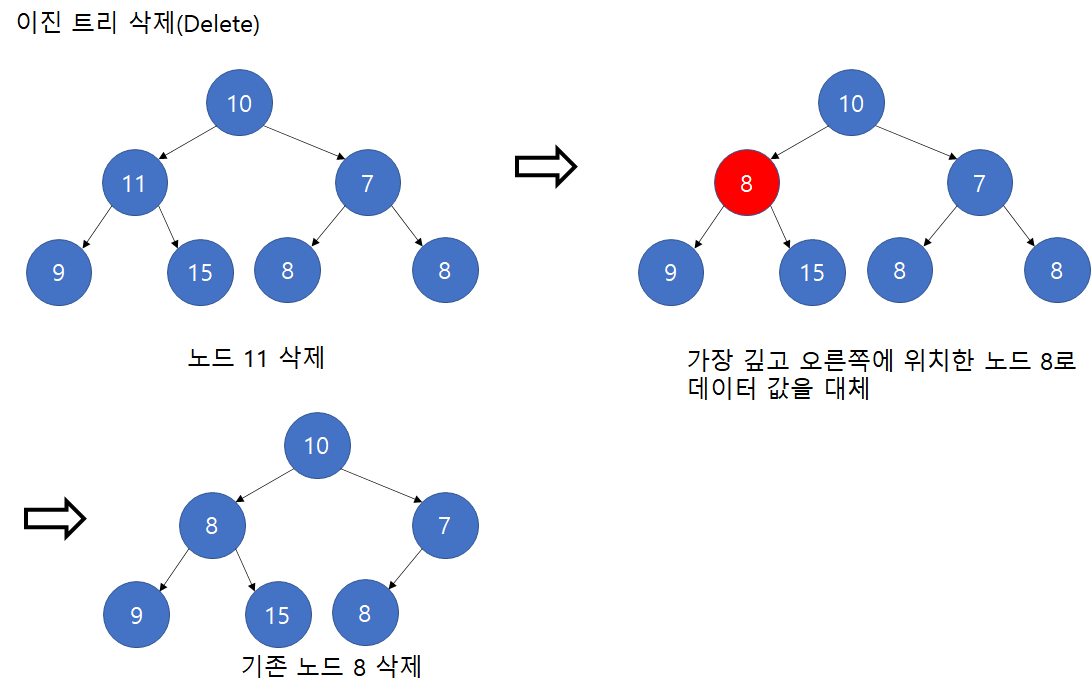
- 시작은 루트 노드(Root Node)에서 시작합니다. 그리고 가장 깊고 오른쪽에 위치한 노드를 탐색하고 삭제하고자 하는 노드를 탐색합니다.
- 삭제하고자 하는 노드에 가장 깊고 오른쪽에 위치한 노드의 데이터 값으로 대체합니다.
- 마지막으로 가장 깊고 오른쪽에 위치한 노드를 삭제합니다.
3. 이진트리 삭제 구현
// 이진 트리 삽입 및 삭제 예제
public class BinaryTree
{
public static class Node
{
int key;
Node left, right;
public Node(int key)
{
this.key = key;
left = right = null;
}
}
Node root;
Node temp = root;
// 비어있는 트리
public BinaryTree()
{
root = null;
}
// 생성자
public BinaryTree(int key)
{
root = new Node(key);
}
// 이진 트리의 중위 순회
private void inorder(Node node)
{
if(node==null)
{
return;
}
inorder(node.left);
System.out.print(node.key+" ");
inorder(node.right);
}
// 이진 트리 중복순회 호출
public void inorderTraversal()
{
inorder(this.root);
System.out.println();
}
// 가장 깊고 오른쪽에 위치한 노드를 삭제
public void deleteDeepest(Node delNode)
{
Queue<Node> q = new LinkedList<Node>();
q.add(root);
Node temp = null;
// 오른쪽 자식 노드만을 계속 참조하면서 delNode를 탐색하고 삭제
while(!q.isEmpty())
{
temp = q.remove();
if(temp==delNode)
{
temp = null;
return;
}
if(temp.right!=null)
{
if(temp.right==delNode)
{
temp.right=null;
return;
}
else {
q.add(temp.right);
}
}
}
if(temp.left!=null)
{
if(temp.left==delNode)
{
temp.left = null;
return;
}
else
{
q.add(temp.left);
}
}
}
// 주어진 key값을 이진트리에서 탐색하여 제거
public void delete(int key)
{
// 이진 트리가 비어있는 경우
if(root==null)
{
return;
}
// 이진트리가 노드가 1개인 경우
if(root.left==null && root.right==null)
{
if(root.key==key) // 루트노드가 삭제하고자 하는 값인 경우
{
root=null;
return;
}
else
{
return;
}
}
Queue<Node> q = new LinkedList<Node>();
q.add(root);
Node temp = null, keyNode = null;
// 레벨 순회 수행
// 삭제할 노드와 가장 오른쪽에 있는 노드를 탐색
// 삭제할 노드는 keyNode에 저장, 가장 오른쪽에 있는 노드는 temp에 저장됨
while(!q.isEmpty())
{
temp = q.remove();
if(temp.key==key)
{
keyNode = temp;
}
if(temp.left!=null)
{
q.add(temp.left);
}
if(temp.right!=null)
{
q.add(temp.right);
}
}
if(keyNode != null) // 삭제하고자 하는 노드를 찾은 경우
{
int x = temp.key; // 가장 깊고 오른쪽에 존재하는 노드가 있음
deleteDeepest(temp);
keyNode.key = x;
}
}
}import org.junit.jupiter.api.Test;
import Tree.BT.Implement.BinaryTree.Node;
class BinaryTreeTest {
@Test
void deleteTest()
{
BinaryTree bt = new BinaryTree();
bt.insert(10);
bt.insert(11);
bt.insert(7);
bt.insert(9);
bt.insert(15);
bt.insert(8);
bt.insert(12);
System.out.print("삭제 이전 중위 순회 : ");
bt.inorderTraversal();
int key = 11;
bt.delete(key);
System.out.print("삭제 이후 중위 순회 : ");
bt.inorderTraversal();
}
}Output
삭제 이전 중위 순회 : 9 11 15 10 8 7 12
삭제 이후 중위 순회 : 9 12 15 10 8 7References
source code : https://github.com/yonghwankim-dev/DataStruct
https://www.geeksforgeeks.org/deletion-binary-tree/
'DataStructure' 카테고리의 다른 글
| 비선형 데이터구조, 트리(Tree) #8 이진 탐색 트리 삭제(Delete) (0) | 2021.09.27 |
|---|---|
| 비선형 데이터구조, 트리(Tree) #7 이진 탐색 트리 탐색(search) 및 추가(add) (0) | 2021.09.24 |
| 비선형 데이터구조, 트리(Tree) #5 이진 트리의 삽입(Insert) (0) | 2021.09.24 |
| 비선형 데이터구조, 트리(Tree) #3 이진 트리의 종류 (0) | 2021.09.23 |
| 비선형 데이터구조, 트리(Tree) #2 이진 트리의 특징 (0) | 2021.09.23 |