2021. 12. 27. 15:39ㆍDataStructure
개요
이번글에서는 AVL 트리에 대해서 소개하겠습니다. AVL 트리가 무엇이고 회전(Rotate) 기능을 통하여 어떻게 트리의 균형(Balance)을 맞추는지 소개합니다.
1. AVL 트리란 무엇인가?
AVL 트리는 이진 탐색 트리를 기반으로 한 트리로써 이진 탐색 트리임에도 불구하고 균형(Balance)이 깨진 트리를 균형있게 맞추어 주는 트리입니다. 대표적인 특징은 왼쪽과 오른쪽의 높이의 차가 항상 1보다 같거나 작아야합니다.
아래의 그림은 균형이 깨진 이진 탐색 트리를 회전을 통하여 균형을 맞추는 그림입니다.
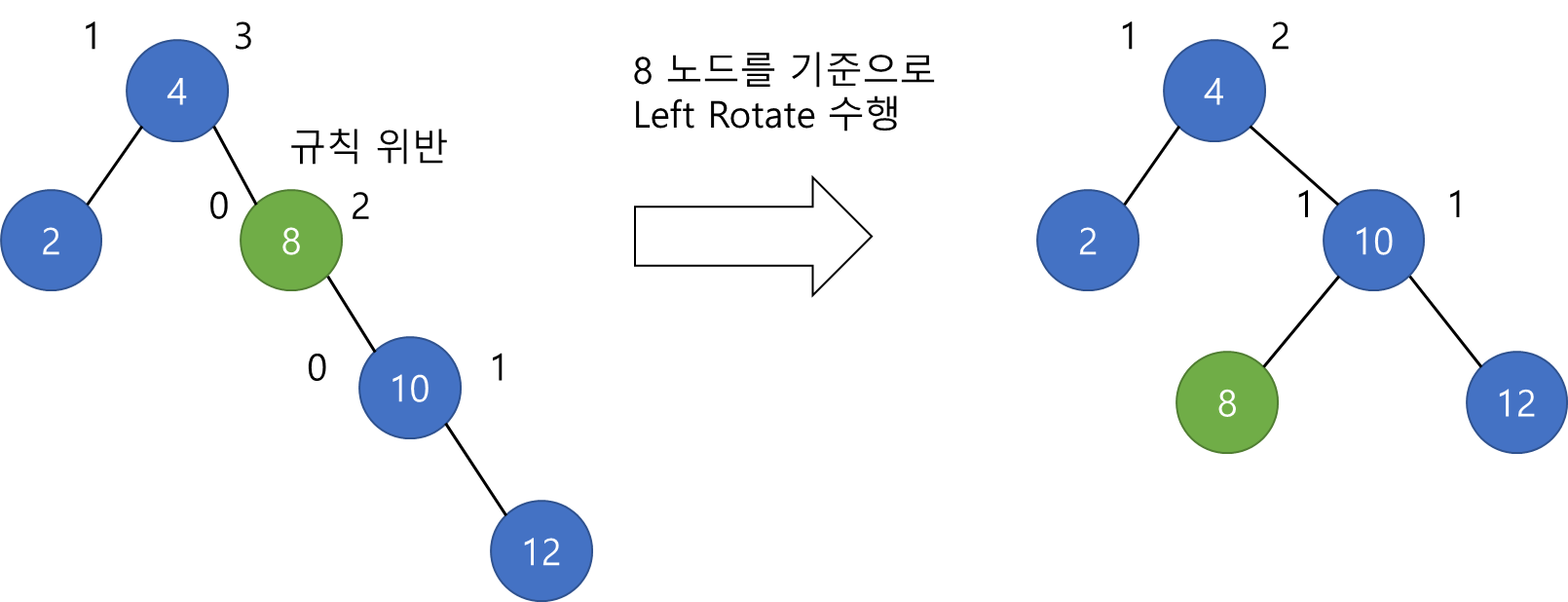
위의 이진 탐색 트리에서 12를 삽입후 8 노드는 왼쪽의 높이가 0이고 오른쪽의 높이가 2이기 때문에 왼쪽과 오른쪽의 높이차가 2가 되버립니다. 위와 같이 높이차가 2 이상인 서브 트리는 불균형한 트리가 됩니다. 따라서 8 노드를 기준으로 왼쪽 회전(Left Rotate)을 수행합니다. 수행 결과 트리의 모든 노드의 높이차가 1이하인 것을 볼 수 있습니다.
이번 예제는 왼쪽 서브트리에서 균형이 깨진 경우입니다.
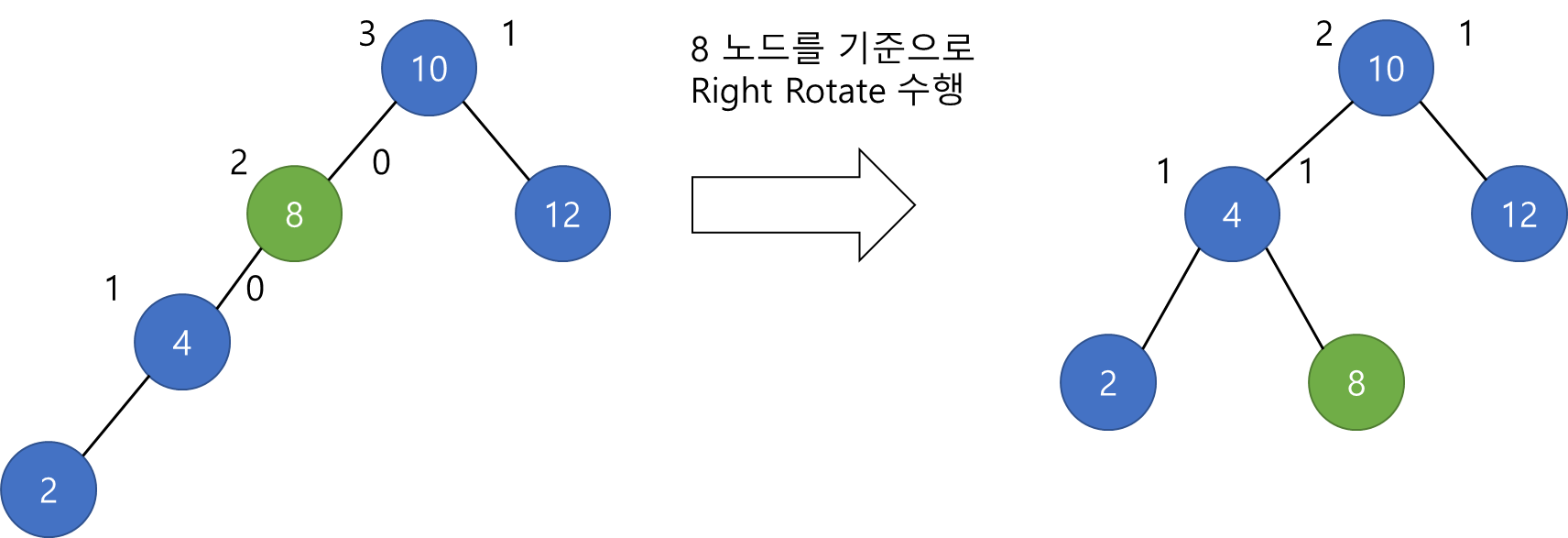
위의 이진 탐색 트리에서 2를 삽입 후 8 노드는 왼쪽 높이가 2이고 오른쪽 높이가 0이기 때문에 왼쪽과 오른쪽의 높이차가 2가 되버립니다. 따라서 위 트리도 불균형가 트리가 됩니다. 따라서 8 노드를 기준으로 오른쪽 회전(Right Rotate)을 수행합니다. 수행한 결과 트리의 모든 노드의 높이차가 1이하인 것을 볼 수 있습니다.
위의 두 예시는 왼쪽 회전(Left Rotate) 또는 오른쪽 회전(Right Rotate)을 한번만 수행한 경우입니다. 아래의 예시와 같이 회전을 두번 사용해야 하는 경우도 존재합니다.
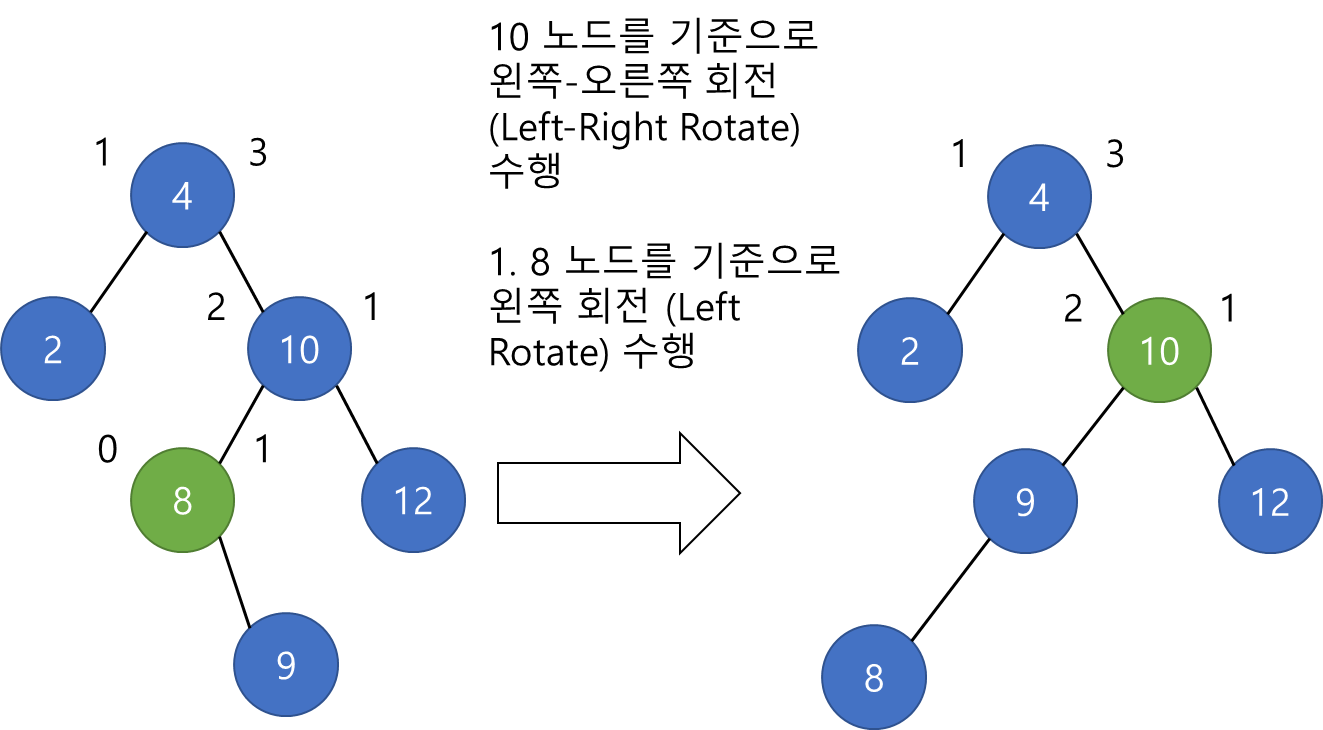
위 트리에서 4 노드가 높이차가 2이므로 10 노드를 기준으로 균형을 맞추어야 합니다. 그리고 10 노드는 단순히 회전을 한번만 수행하는 것이 아닌 왼쪽-오른쪽 회전을 수행해야지 균형을 맞출 수 있습니다. 따라서 8 노드를 기준으로 왼쪽 회전(Left Rotate)을 수행하고 다시 10 노드를 기준으로 오른쪽 회전을 수행합니다. 오른쪽 회전을 수행한 결과는 아래와 같습니다.

오른쪽 회전을 수행한 결과는 위 그림의 오른쪽 트리와 같습니다. 그런데 여전히 4 노드의 높이차는 2이기 때문에 다시 4노드를 기준으로 왼쪽 회전(Left Rotate)를 수행하여 균형을 맞춥니다.

위 수행 결과에 따라 루트 노드까지의 높이차가 전부 1 이하이므로 수행을 종료합니다.
2. AVL 트리의 노드 구현
이진 탐색 트리의 노드는 값을 담을 수 있는 data, 왼쪽 자식을 가리키는 left 노드, 오른쪽 자식을 가리키는 right 노드가 필요했었습니다. AVL 트리에서는 이에 더해서 부모 노드를 가리키는 parent 노드를 추가합니다. parent 포인터 노드는 트리의 균형을 편하게 맞추기 위해서 추가합니다.
class Node<T>{
T data;
Node<T> left;
Node<T> right;
Node<T> parent;
// 생성자
public Node(T obj){
data = obj;
parent = left = right = null;
}3. add 메서드
public class AVLTree<T> {
private Node<T> root;
int currentSize;
...
public AVLTree() {
root = null;
currentSize = 0;
}
public void add(T obj) {
Node<T> node = new Node<T>(obj);
// 트리가 비었을 경우
if(root==null)
{
root = node;
currentSize++;
return;
}
else
{
add(root, node);
}
}
private void add(Node<T> root, Node<T> newNode)
{
// newNode의 data가 root의 data보다 작은 경우
if(((Comparable<T>)newNode).compareTo(root.data)<=0)
{
if(root.left==null)
{
root.left = newNode;
newNode.parent = root;
currentSize++;
}
else
{
add(root.left, newNode);
}
}
// newNode의 data가 root의 data보다 큰 경우
else
{
if(root.right==null)
{
root.right = newNode;
newNode.parent = root;
currentSize++;
}
else
{
add(root.right, newNode);
}
}
// AVL 트리가 규칙에 맞게 잘 되었는지 검사합니다.
checkBalance(newNode);
}
private void checkBalance(Node<T> newNode) {
return;
}
}
References
source code : https://github.com/yonghwankim-dev/DataStruct/tree/main/Tree/avltree
[부스트코스] 자바로 구현하고 배우는 자료구조
'DataStructure' 카테고리의 다른 글
| 비선형 데이터구조, RedBlackTree #1 RedBlackTree의 규칙 및 수행과정 (0) | 2021.12.29 |
|---|---|
| 비선형 데이터구조, AVL Tree #2 AVL 트리 checkBalance & rebalance 메서드 (0) | 2021.12.28 |
| 비선형 데이터구조, 트리(Tree) #10 이진탐색트리의 회전(Rotate) (0) | 2021.12.24 |
| 비선형 데이터구조, 트리(Tree) #4 이진 트리의 순회 및 표현식 (0) | 2021.12.20 |
| 비선형 데이터구조, 힙(Heap) #2 이진 힙 정렬(Binary Heap Sort) (0) | 2021.12.16 |