2021. 10. 6. 12:15ㆍCodingTest
1. 문제
https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
2. 문제요약
- 계단 오르기 규칙
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
- 위의 계단 오르기 규칙을 준수하면서 계단 오르기 게임에서 얻을 수 있는 점수의 최댓값을 출력
- 계단의 개수인 n의 범위는 1<=n<=300, 1<=계단의 점수<=10,000
3. 문제풀이
위 문제는 동적 계획법을 적용하여 해결해야 합니다. 문제의 핵심은 마지막 계단인 N번째 계단을 무조건 밟아야 한다는 점이고 N번째 계단을 밟기 이전의 경우의 수는 대표적으로 2가지가 존재합니다.
1. N-1번째 계단을 밟은 경우
- N-2번째 계단은 밟지 못하므로(연속 3계단을 오르지 못하는 규칙) N번째 계단 값, N-1번째 계단 값, N-3번째 계단까지의 값을 합산합니다. 이와 같은 점화식은 아래와 같습니다.
-
dp[i] = arr[n] + arr[n-1] + dp[i-3]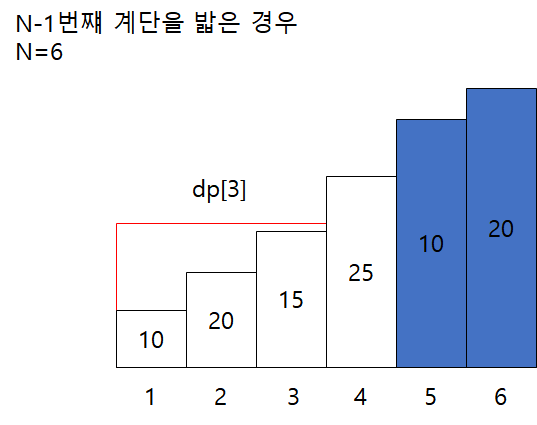
dp[3]의 3번째 계단이 마지막 계단이라 가정하고, 3번째 계단까지 밟는데 나올 수 있는 최댓값을 의미합니다.
위의 그림에서 3번째 계단까지 밟는데 나올 수 있는 나올 수 있는 경우의 수는 2번째 계단을 밟거나 밟지 않는 경우에 따른 2가지 케이스입니다. 2가지 케이스를 계산하면 2번째 계단을 밟는 경우는 20+15=35이고 2번째 계단을 밟지 않는 경우는 10+15=25이므로 2번째 계단을 밟는 경우가 3번째 계단을 밟았을때 값이 높습니다. 그러므로 dp[3]=35입니다.
따라서 N=6인 계단인 위의 그림에서 5번째 계단을 밟아서 나올 수 있는 값은 dp[6] = dp[3] + arr[5] + arr[6] = 35 + 10 + 20 = 65입니다. 정리하면 N-1번째 계단을 밟은 경우 6번째 계단을 밟았을때 나오는 누적합은 65입니다.
2. N-1번째 계단을 밟지 않은 경우
- N-2번째 계단을 밟았으므로 N번째 계단 값, N-2번째 계단까지의 값을 합산합니다. 이와 같은 점화식은 아래와 같습니다.
-
dp[n] = arr[n] + dp[n-2]
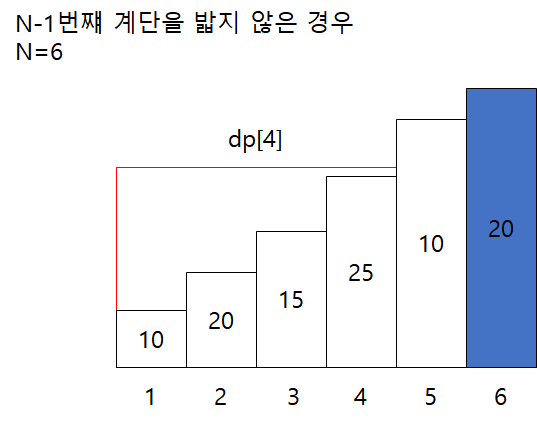
5번째 계단을 밟지 않는 경우 4번째 계단을 무조건 밟아야 합니다. 이는 N=4라고 가정하고 4번째 계단이 마지막 계단이라 생각하고 4번째 계단을 밟았을 때 나오는 최댓값을 구하여야 합니다. 이를 dp[4]로 표현하고 N=6일때 점화식을 생각하면 dp[6] = arr[6] + dp[4]로 표현이 가능합니다.
위의 2가지 케이스에 대한 값이 2개 나오는데 둘 중 최댓값이 문제에서 원하는 정답입니다.
4. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static int[] dp;
static int[] arr;
private static int recursion(int i)
{
if(i<=0)
{
return 0;
}
int var1 = 0;
int var2 = 0;
if(i>=3)
{
var1 = (dp[i-3]==0 ? recursion(i-3) : dp[i-3]);
var2 = (dp[i-2]==0 ? recursion(i-2) : dp[i-2]);
}
return dp[i] = Math.max(
arr[i] + arr[i-1] + var1,
arr[i] + var2
);
}
public static int solution(int n)
{
// 마지막 계단 이전 계단을 밟은 경우
int var1 = arr[n] + arr[n-1] + recursion(n-3);
// 마지막 계단 이전 계단을 밟지 않은 경우
int var2 = arr[n] + recursion(n-2);
// 위의 두가지 경우중 값이 큰것을 반환
return Math.max(var1, var2);
}
public static void main(String args[]) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
arr = new int[n+1];
dp = new int[n+1];
for(int i=1;i<=n;i++)
{
arr[i] = Integer.parseInt(br.readLine());
}
System.out.println(solution(n));
}
}
References
https://mygumi.tistory.com/100
'CodingTest' 카테고리의 다른 글
| 백준 1929, 소수 구하기 (0) | 2021.10.21 |
|---|---|
| 백준 11053, 가장 긴 증가하는 부분 수열 (0) | 2021.10.14 |
| 백준 1149, RGB 거리 (0) | 2021.10.05 |
| 백준 15649, N과 M (1) (0) | 2021.09.22 |
| 백준 2193, 이천수 (0) | 2021.09.13 |